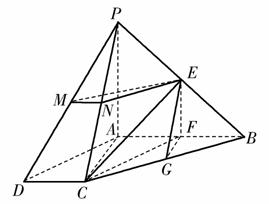
如图，四棱锥P－ABCD中，AB⊥AC，AB⊥PA，AB∥CD，AB＝2CD，E，F，G，M，N分别为PB，AB，BC，PD，PC的中点．
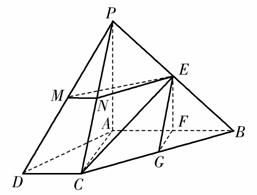
(1)求证：CE∥平面PAD；
(2)求证：平面EFG⊥平面EMN.
[解析] (1)解法一：取PA的中点H，连接EH，DH.
因为E为PB的中点，
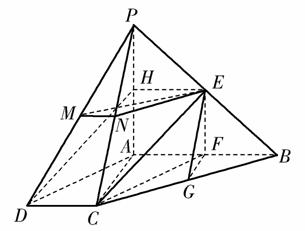
所以EH∥AB，EH＝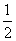
AB.
又AB∥CD，CD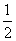＝AB，所以EH∥CD，EH＝CD.
因此四边形DCEH是平行四边形．所以CE∥DH.
又DH⊂平面PAD，CE⊄平面PAD，
因此CE∥平面PAD.
解法二：连接CF.
因为F为AB的中点，所以AF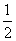＝AB.
又CD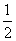＝AB，所以AF＝CD.
又AF∥CD，所以四边形AFCD为平行四边形．
因此CF∥AD.
又CF⊄平面PAD，所以CF∥平面PAD.
因为E、F分别为PB、AB的中点，所以EF∥PA.
又EF⊄平面PAD，所以EF∥平面PAD.
因为CF∩EF＝F，故平面CEF∥平面PAD.
又CE⊂平面CEF，所以CE∥平面PAD.
(2)证明：因为E、F分别为PB、AB的中点，
所以EF∥PA.
又AB⊥PA，所以AB⊥EF.
同理可证AB⊥FG.
又EF∩FG＝F，EF⊂平面EFG，FG⊂平面EFG，
因此AB⊥平面EFG.
又M、N分别为PD、PC的中点，
所以MN∥CD.
又AB∥CD，所以MN∥AB.
因此MN⊥平面EFG.
又MN⊂平面EMN，
所以平面EFG⊥平面EMN.
科目：高中数学 来源： 题型：
已知直线m、n与平面α、β，下列命题中正确的是( )
A．m∥β，α∥β，则m∥α
B．平面α内不共线三点到平面β的距离相等，则α∥β
C．α∩β＝m，n⊥m且α⊥β，则n⊥α
D．m⊥α，n⊥β且α⊥β，则m⊥n
查看答案和解析>>
科目：高中数学 来源： 题型：
设a、b是两条不同的直线，α、β是两个不同的平面，则下列命题错误的是( )
A．若a⊥α，b∥α，则a⊥b
B．若a⊥α，b∥a，b⊂β，则α⊥β
C．若a⊥α，b⊥β，α∥β，则a∥b
D．若a∥α，a∥β，则α∥β
查看答案和解析>>
科目：高中数学 来源： 题型：
如图，在多面体ABCDEF中，四边形ABCD是正方形，AB＝2EF＝2，EF∥AB，EF⊥FB，∠BFC＝90°，BF＝FC，H为BC的中点．
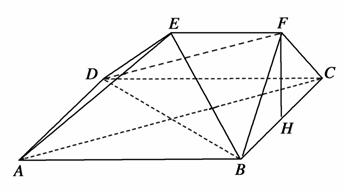
(1)求证：FH∥平面EDB；
(2)求证：AC⊥平面EDB；
(3)求四面体B－DEF的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
下列四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥平面MNP的图形的序号是______(写出所有符合要求的图形序号)．
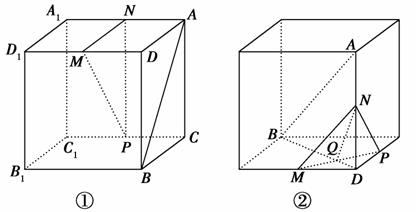
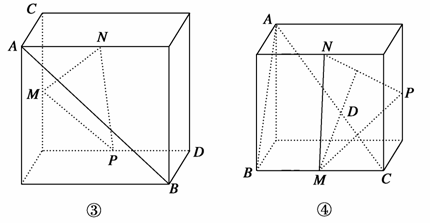
查看答案和解析>>
科目：高中数学 来源： 题型：
设a、b为两条直线，α、β为两个平面，下列四个命题中真命题是( )
A．若a、b与α所成角相等，则a∥b
B．若a∥α，b∥β，α⊥β，则a⊥b
C．若a⊂α，b⊂β，a⊥b，则α⊥β
D．若a⊥α，b⊥β，α⊥β，则a⊥b
查看答案和解析>>
科目：高中数学 来源： 题型：
定点A和B都在平面α内，定点P∉α，PB⊥α，C是α内异于A和B的动点，且PC⊥AC.那么，动点C在平面α内的轨迹是( )
A．一条线段，但要去掉两个点
B．一个圆，但要去掉两个点
C．一个椭圆，但要去掉两个点
D．半圆，但要去掉两个点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则其侧面展开图中心角α满足( )
(AC＋BD)(填“>”，“<”或“＝”)．