
分析 (Ⅰ)求出原函数的导函数,得到导函数的零点,利用函数f(x)在x=2处取得极值,得到a-1=2,从而求得实数a的值;
(Ⅱ)把对任意x1∈[$\frac{1}{e}$,1],总存在x2∈[$\frac{1}{e}$,1],使得g(x1)=f(x2)成立转化为函数f(x)在[$\frac{1}{e}$,1]上的值域为g(x)在[$\frac{1}{e}$,1]上的值域的子集,利用f(x)、g(x)的单调性求其值域,然后利用两个函数值域端点值间的关系列不等式组求得答案.
解答 解:(Ⅰ)由f(x)=x-alnx+$\frac{1-a}{x}$,(x>0),
得f′(x)=1-$\frac{a}{x}$-$\frac{1-a}{{x}^{2}}$=$\frac{{x}^{2}-ax+a-1}{{x}^{2}}$,
由x2-ax+a-1=0,得x1=1,x2=a-1,
∵函数f(x)在x=2处取得极值,∴a-1=2,即a=3;
(Ⅱ)假设存在a∈(3,+∞),对任意x1∈[$\frac{1}{e}$,1],总存在x2∈[$\frac{1}{e}$,1],使得g(x1)=f(x2)成立.
则函数f(x)在[$\frac{1}{e}$,1]上的值域为g(x)在[$\frac{1}{e}$,1]上的值域的子集,
由(Ⅰ)知,f(x)在[$\frac{1}{e}$,1]上为增函数,
∴f(x)∈[$\frac{1}{e}$+a+e-ae,2-a],
又g(x)=x-1在[$\frac{1}{e}$,1]上为增函数,
∴g(x)∈[$\frac{1}{e}$-1,0],
则 $\left\{\begin{array}{l}{\frac{1}{e}+a+e-ae≤2-a}\\{\frac{1}{e}-1≤\frac{1}{e}+a+e-ae}\\{2-a≤0}\end{array}\right.$,解得:2≤a≤$\frac{e+1}{e-1}$.
而$\frac{e+1}{e-1}$<3,
∴不存在a∈(3,+∞),对任意x1∈[$\frac{1}{e}$,1],总存在x2∈[$\frac{1}{e}$,1],使得g(x1)=f(x2)成立.
点评 本题考查了利用导数研究函数的极值,考查数学转化思想方法,正确理解题意是解答(Ⅱ)的关键,是压轴题.


 培优口算题卡系列答案
培优口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
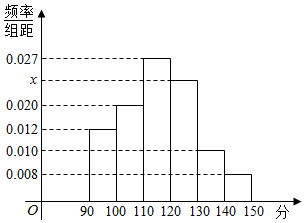 某校高一年级为组建数学兴趣小组,对参加报名的100名同进行了摸底考试,发现其成绩都在90-150分之间.频率分布直方图如图所示
某校高一年级为组建数学兴趣小组,对参加报名的100名同进行了摸底考试,发现其成绩都在90-150分之间.频率分布直方图如图所示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{4}{15}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com