
 ijУ��һ�꼶Ϊ�齨��ѧ��ȤС�飬�Բμӱ�����100��ͬ�����������ԣ�������ɼ�����90-150��֮�䣮Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ
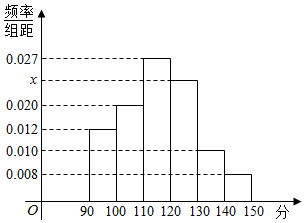
ijУ��һ�꼶Ϊ�齨��ѧ��ȤС�飬�Բμӱ�����100��ͬ�����������ԣ�������ɼ�����90-150��֮�䣮Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���� ��1������Ƶ�ʷֲ�ֱ��ͼ�����x��ֵ����������ֵ������100��ͬѧ��ƽ���÷֣�
��2��ȷ������5�ˣ�Ů��3�ˣ����������֪ѡȡ��1��ΪŮ���������£���2�˳ɼ���149�ֵĸ��ʣ�
��� �⣺��1������Ƶ�ʷֲ�ֱ��ͼ���ã�0.012+0.02+0.027+x+0.01+0.008����10=1��
��x=0.023��
��100��ͬѧ��ƽ���÷֣�0.012��95+0.02��105+0.027��115+0.023��125+0.01��135+0.008��145����10=117.3��
��2��0.008��10��100=8��������������[140.150���ڵ���������Ů����Ϊ5��3��
������5�ˣ�Ů��3��
����֪ѡȡ��1��ΪŮ���������£���2�˳ɼ���149�ֵĸ���Ϊ$\frac{{C}_{6}^{1}+{C}_{2}^{1}{C}_{4}^{1}}{{C}_{8}^{3}}$=$\frac{1}{4}$��
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ��Ӧ�����⣬����ʱ��Ӧ��ͼ�ν���й���Ƶ�ʡ�Ƶ����ƽ���������⣬�ǻ����⣮


 Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | -1 | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��-1����f��-2����f��-3�� | B�� | f��-3����f��-2����f��-1�� | C�� | f��-2����f��-1����f��-3�� | D�� | f��-3����f��-1����f��-2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
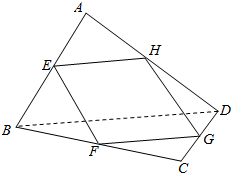 ��֪���ռ��ı���ABCD�У�E��F��G��H�ֱ�ΪAB��BC��CD��DA���е㣮��֤��E��F��G��H�ĵ㹲�棨��ͼ��ʾ��
��֪���ռ��ı���ABCD�У�E��F��G��H�ֱ�ΪAB��BC��CD��DA���е㣮��֤��E��F��G��H�ĵ㹲�棨��ͼ��ʾ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com