
分析 根据函数f(x0的定义域为(0,+∞),得到函数在定义域内的最小值为1,则答案得证.
解答 证明:∵f(x)=exln x+$\frac{2}{x}$ex-1,
从而f(x)>1等价于xln x>xe-x-$\frac{2}{e}$.
设函数g(x)=xln x,
则g′(x)=1+ln x,
所以当x∈(0,$\frac{1}{e}$)时,g′(x)<0;
当x∈($\frac{1}{e}$,+∞)时,g′(x)>0.
故g(x)在(0,$\frac{1}{e}$)上单调递减,在($\frac{1}{e}$,+∞)上单调递增,
从而g(x)在(0,+∞)上的最小值为g($\frac{1}{e}$)=-$\frac{1}{e}$.
设函数h(x)=xe-x-$\frac{2}{e}$,则h′(x)=e-x(1-x).
所以当x∈(0,1)时,h′(x)>0;
当x∈(1,+∞)时,h′(x)<0.
故h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
从而h(x)在(0,+∞)上的最大值为h(1)=-$\frac{1}{e}$;
因为gmin(x)=h(1)=hmax(x),
所以当x>0时,g(x)>h(x),即f(x)>1.
点评 本题考查了导数的应用,考查函数的单调性问题,考查了利用导数求函数的最值,是中高档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
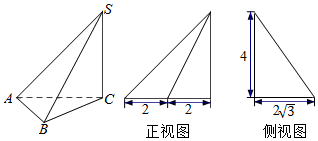
| A. | $16\sqrt{3}$ | B. | $\sqrt{38}$ | C. | $4\sqrt{2}$ | D. | $2\sqrt{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
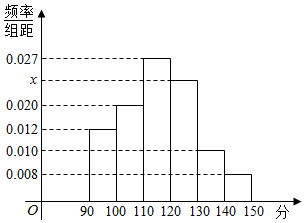 某校高一年级为组建数学兴趣小组,对参加报名的100名同进行了摸底考试,发现其成绩都在90-150分之间.频率分布直方图如图所示
某校高一年级为组建数学兴趣小组,对参加报名的100名同进行了摸底考试,发现其成绩都在90-150分之间.频率分布直方图如图所示查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{4}{15}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com