
分析 (1)根据二倍角公式可以化简f(x)得到f(x)=$a(1+cos2x)+\sqrt{3}bsin2x$,根据f(0)=2,$f(\frac{π}{4})=\sqrt{3}+1$便可求出a=1,b=1,从而得出$f(x)=2sin(2x+\frac{π}{6})+1$,容易得到f(x)的最大值为3,而根据正弦函数的单调性便可得出该函数的单调递减区间;
(2)根据条件得到$sin(2α+\frac{π}{6})=sin(2β+\frac{π}{6})$,而$2α+\frac{π}{6}≠2β+\frac{π}{6}$,且$2α+\frac{π}{6},2β+\frac{π}{6}∈(\frac{π}{6},\frac{13π}{6})$,从而便可得到$2α+\frac{π}{6}+2β+\frac{π}{6}=π$,或3π,进一步便可得出α+β的值,从而可求出tan(α+β)的值.
解答 解:$f(x)=a(1+cos2x)+\sqrt{3}bsin2x$;
∴f(0)=2a=2;
∴a=1;
又$f(\frac{π}{4})=a+\sqrt{3}b=1+\sqrt{3}b=\sqrt{3}+1$;
∴b=1;
∴$f(x)=1+cos2x+\sqrt{3}sin2x$=$2sin(2x+\frac{π}{6})+1$;
∴(1)$2x+\frac{π}{6}=\frac{π}{2}+2kπ,k∈Z$,即$x=\frac{π}{6}+kπ,k∈Z$时,f(x)取得最大值3;
令$\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{3π}{2}+2kπ,k∈Z$得,$\frac{π}{6}+kπ≤x≤\frac{2π}{3}+kπ,k∈Z$;
∴f(x)的单调递减区间为$[\frac{π}{6}+kπ,\frac{2π}{3}+kπ],k∈Z$;
(2)由f(α)=f(β)得,$sin(2α+\frac{π}{6})=sin(2β+\frac{π}{6})$;
∵α≠β,α,β∈(0,π);
∴$2α+\frac{π}{6}≠2β+\frac{π}{6}$,$2α+\frac{π}{6}∈(\frac{π}{6},\frac{13π}{6}),2β+\frac{π}{6}∈(\frac{π}{6},\frac{13π}{6})$;
∴$(2α+\frac{π}{6})+(2β+\frac{π}{6})=π$,或3π;
∴$α+β=\frac{π}{3}$,或$\frac{4π}{3}$;
∴$tan(α+β)=\sqrt{3}$.
点评 考查二倍角的正余弦公式,两角和的正弦公式,以及正弦函数的最大值和单调区间,清楚α≠β时,由sinα=sinβ得到α+β=(2n+1)π,n∈Z.


科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤1} | B. | {x|-1≤x<0} | C. | {x|x<-1} | D. | {x|x≥-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{A{C}_{1}}$ | B. | $\overrightarrow{C{A}_{1}}$ | C. | $\overrightarrow{B{C}_{1}}$ | D. | $\overrightarrow{C{B}_{1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
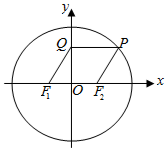 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,过椭圆上的点P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该椭圆的离心率为( )
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,过椭圆上的点P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该椭圆的离心率为( )| A. | $\frac{{\sqrt{2}-1}}{2}$ | B. | $\frac{{\sqrt{3}-1}}{2}$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com