练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．若集合A={x|-1≤x≤1}，B={x|x≥0}，则A∩B=（　　）
    A．{x|0≤x≤1}B．{x|-1≤x＜0}C．{x|x＜-1}D．{x|x≥-1}

    分析 根据集合的基本运算进行求解．

    解答 解：∵A={x|-1≤x≤1}，B={x|x≥0}，
    ∴A∩B={x|0≤x≤1}，
    故选：A．

    点评 本题主要考查集合的基本运算，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

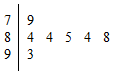    9．如图，是2007年在广州举行的全国少数民族运动会上，七位评委为某民族舞蹈打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（　　）
    A．84，4.84B．84，1.6C．85，2.4D．85，1.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

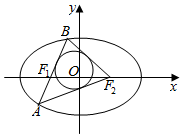    10． 如图，设椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左右焦点分别为F1、F2，过焦点F1的直线交椭圆于A、B两点，若以△ABF2的内切圆的面积为π，设A（x1，y1）、B（（x2，y2），则|y1-y2|值为$\frac{10}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．命题：“若a≥b，则2a≥2b”的逆否命题为若2a＜2b，则a＜b．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知圆A：（x+2）2+y2=1，圆B：（x-2）2+y2=49，动圆P与圆A，圆B均相切．
    （1）求动圆圆心P的轨迹方程；
    （2）已知点N（2，$\frac{5}{3}$），作射线AN，与“P点 轨迹”交于另一点M，求△MNB的周长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．某校的一个社会实践调查小组，在对该校学生的良好“用眼习惯”的调查中，随机发放了120分问卷．对收回的100份有效问卷进行统计，得到如2×2下列联表：
    做不到科学用眼能做到科学用眼合计
    男451055
    女301545
    合计7525100
    （1）现按女生是否能做到科学用眼进行分层，从45份女生问卷中抽取了6份问卷，从这6份问卷中再随机抽取3份，并记其中能做到科学用眼的问卷的份数X，试求随机变量X的分布列和数学期望；
    （2）若在犯错误的概率不超过P的前提下认为良好“用眼习惯”与性别有关，那么根据临界值表，最精确的P的值应为多少？请说明理由．
    附：独立性检验统计量${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
    独立性检验临界值表：
    P（K2≥k0）0.250.150.100.050.025
    k01.3232.0722.7063.8405.024

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

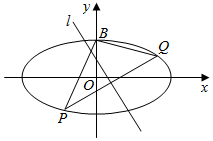    11．已知中心在原点O，焦点在x轴上的椭圆的一个顶点为B（0，1），B到焦点的距离为2．
    （Ⅰ）求椭圆的标准方程；
    （Ⅱ）设P，Q是椭圆上异于点B的任意两点，且BP⊥BQ，线段PQ的中垂线l与x轴的交点为（x0，0），求x0的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知椭圆$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1的两焦点分别为F1，F2，过F1的直线与椭圆交于A，B两点，则△ABF2的周长为8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=2acos2x+2$\sqrt{3}$bsinxcosx，且f（0）=2，f（$\frac{π}{4}$）=$\sqrt{3}$+1．
    （1）求f（x）的最大值及单调递减区间；
    （2）若α≠β，α，β∈（0，π），且f（α）=f（β），求tan（α+β）的值．

    查看答案和解析>>

    同步练习册答案