
| 做不到科学用眼 | 能做到科学用眼 | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
分析 (1)分层从45份女生问卷中抽取了6份问卷,其中“科学用眼”抽6×$\frac{15}{45}$=2人,“不科学用眼”抽$6×\frac{30}{45}$=4人,若从这6份问卷中随机抽取3份,随机变量X=0,1,2.利用“超几何分布”即可得出分布列及其数学期望;
(2)根据“独立性检验的基本思想的应用”计算公式可得K2的观测值k,即可得出.
解答 解:(1)“科学用眼”抽6×$\frac{15}{45}$=2人,“不科学用眼”抽$6×\frac{30}{45}$=4人.…(2分)
则随机变量X=0,1,2,…(3分)
∴$P(X=0)=\frac{C_4^3}{C_6^3}=\frac{4}{20}$=$\frac{1}{5}$;$P(X=1)=\frac{C_2^1C_4^2}{C_6^3}=\frac{12}{20}$=$\frac{3}{5}$;$P(X=2)=\frac{C_2^2C_4^1}{C_6^3}=\frac{4}{20}$=$\frac{1}{5}$…(6分)
分布列为
| X | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查了组合数的计算公式、古典概率计算公式、“超几何分布”分布列及其数学期望公式、“独立性检验的基本思想的应用”计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{\sqrt{3}}{2}$,1) | B. | [$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$] | C. | [$\frac{\sqrt{2}}{2}$,1) | D. | [$\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤1} | B. | {x|-1≤x<0} | C. | {x|x<-1} | D. | {x|x≥-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
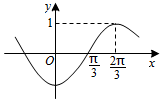
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
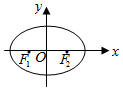 平面直角坐标系xOy中,已知F1、F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且右焦点F2的坐标为($\sqrt{3}$,0),点($\sqrt{3}$,$\frac{1}{2}$)在椭圆C上.
平面直角坐标系xOy中,已知F1、F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且右焦点F2的坐标为($\sqrt{3}$,0),点($\sqrt{3}$,$\frac{1}{2}$)在椭圆C上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com