
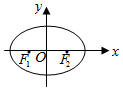
 ƽ��ֱ������ϵxOy�У���֪F1��F2�ֱ�����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬���ҽ���F2������Ϊ��$\sqrt{3}$��0�����㣨$\sqrt{3}$��$\frac{1}{2}$������ԲC�ϣ�
ƽ��ֱ������ϵxOy�У���֪F1��F2�ֱ�����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬���ҽ���F2������Ϊ��$\sqrt{3}$��0�����㣨$\sqrt{3}$��$\frac{1}{2}$������ԲC�ϣ����� ����������Բ�Ľ�������͵�����ԲC�ϣ��г������飬���a��b���ɴ��������Բ�ı����̣�
����1����P��2cos�ȣ�sin�ȣ�����Q��4cos�ȣ�2sin�ȣ���0�ܦȣ�2�У��ɴ����������P����ԲC���˶�ʱ�����Q�γɵĹ켣E�ķ��̣�
��2������$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1}\end{array}\right.$����5x2+8mx+4m2-16=0���ɴ����ø����б�ʽ��Τ�ﶨ�����ҳ���ʽ���㵽ֱ�߾��빫ʽ�������֪�������ABQ��������ֵ��
��� �⣺����F1��F2�ֱ�����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬
���ҽ���F2������Ϊ��$\sqrt{3}$��0�����㣨$\sqrt{3}$��$\frac{1}{2}$������ԲC�ϣ�
��$\left\{\begin{array}{l}{c=\sqrt{3}}\\{\frac{3}{{a}^{2}}+\frac{1}{4{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$�����a=2��b=1��
����ԲC�ı�����Ϊ$\frac{{x}^{2}}{4}$+y2=1��
����1��������ԲC����ȡһ��P����Q��PO���ӳ����ϣ���$\frac{|OQ|}{|OP|}$=2��
����P��2cos�ȣ�sin�ȣ�����Q��4cos�ȣ�2sin�ȣ���0�ܦȣ�2�У�
�൱��P����ԲC���˶�ʱ�����Q�γɵĹ켣E�ķ��̣�
$\left\{\begin{array}{l}{x=4cos��}\\{y=2sin��}\end{array}\right.$��0�ܦȣ�2�У�
���E��ֱ�����귽��Ϊ��$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}$=1��
��2������$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1}\end{array}\right.$����5x2+8mx+4m2-16=0��
��A��x1��y1����B��x2��y2������${x}_{1}+{x}_{2}=-\frac{8m}{5}$��${x}_{1}{x}_{2}=\frac{4{m}^{2}-16}{5}$��
��=64m2-80m2+320��0�����-2$\sqrt{5}��m��2\sqrt{5}$��
|AB|=$\sqrt{2[��-\frac{8m}{5}��^{2}-4��\frac{4{m}^{2}-16}{5}]}$=$\frac{4}{5}\sqrt{10-{m}^{2}}$��
��Q��ֱ��y=x+m�ľ���d=$\frac{|{x}_{Q}-{y}_{Q}+m|}{\sqrt{2}}$��
��xQ=2xP��yQ=2yP��=2��xP+m����
��$\frac{|2{x}_{P}-2{x}_{P}-2m+m|}{\sqrt{2}}$=$\frac{|m|}{\sqrt{2}}$��
����$\left\{\begin{array}{l}{y=x+n}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$����5x2+8mx+4m2-4=0��
��=80-16m2��0����m2��5��
��${S}_{��ABQ}=\frac{1}{2}d•|AB|$=$\frac{1}{2}��\frac{|m|}{\sqrt{2}}��\sqrt{2}��\frac{\sqrt{320-16{m}^{2}}}{5}$
=$\frac{2}{5}\sqrt{-{m}^{4}+20{m}^{2}}$=$\frac{2}{5}\sqrt{-��{m}^{2}-10��^{2}+100}$��
��m2=5ʱ��S��ABQ�����S��ABQ���ֵΪ2$\sqrt{3}$��
���� ���⿼����Բ���̵���������������������ֵ�������е��⣬����ʱҪ�������⣬ע������б�ʽ��Τ�ﶨ�����ҳ���ʽ���㵽ֱ�߾��빫ʽ�ĺ������ã�


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
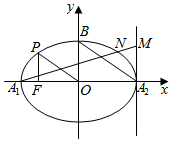 ��ͼ����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������Ҷ���ֱ�ΪA1��A2���϶���ΪB������Բ��һ��P��x�������ߣ�����ǡΪ��F����A2B��OP��|FA2|=$\sqrt{10}$+$\sqrt{5}$����A2��x��Ĵ���l����M��l������һ�㣬A1M����Բ�ڵ�N����$\overrightarrow{OM}$•$\overrightarrow{ON}$=��������
��ͼ����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������Ҷ���ֱ�ΪA1��A2���϶���ΪB������Բ��һ��P��x�������ߣ�����ǡΪ��F����A2B��OP��|FA2|=$\sqrt{10}$+$\sqrt{5}$����A2��x��Ĵ���l����M��l������һ�㣬A1M����Բ�ڵ�N����$\overrightarrow{OM}$•$\overrightarrow{ON}$=��������| A�� | 10 | B�� | 5 | ||
| C�� | 15 | D�� | ���M��ֱ��l�ϵ�λ�ñ仯���仯 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��������ѧ���� | ��������ѧ���� | �ϼ� | |
| �� | 45 | 10 | 55 |
| Ů | 30 | 15 | 45 |
| �ϼ� | 75 | 25 | 100 |
| P��K2��k0�� | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x���ڣ�0��+�ޣ����м���ֵ$\frac{1}{2}$ | B�� | f��x���ڣ�0��+�ޣ����м�Сֵ$\frac{1}{2}$ | ||
| C�� | f��x���ڣ�0��+�ޣ��������� | D�� | f��x���ڣ�0��+�ޣ������ݼ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
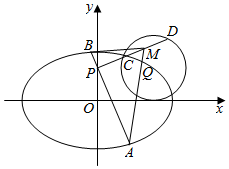 ��֪F1��F2Ϊ��Բ${C_1}��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$�����ҽ��㣬F2����$Q��\sqrt{2}��1��$ΪԲ�ģ�1Ϊ�뾶��ԲC2�ϣ���|QF1|+|QF2|=2a��
��֪F1��F2Ϊ��Բ${C_1}��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$�����ҽ��㣬F2����$Q��\sqrt{2}��1��$ΪԲ�ģ�1Ϊ�뾶��ԲC2�ϣ���|QF1|+|QF2|=2a���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com