
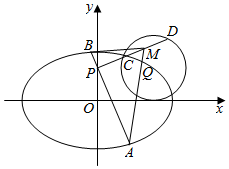
 已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F2在以$Q(\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F2在以$Q(\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.分析 (Ⅰ)圆C2的方程为${(x-\sqrt{2})^2}+{(y-1)^2}=1$,由此圆与x轴相切,求出a,b的值,由此能求出椭圆C1的方程.
(Ⅱ)设l1:x=t(y-1),则l2:tx+y-1=0,与椭圆联立,得(t2+2)y2-2t2y+t2-4=0,由此利用弦长公式、点到直线距离公式,结合已知条件能求出△MAB面积的取值范围.
解答 (本题满分15分)
解:(Ⅰ)圆C2的方程为${(x-\sqrt{2})^2}+{(y-1)^2}=1$,
此圆与x轴相切,切点为$(\sqrt{2},0)$
∴$c=\sqrt{2}$,即a2-b2=2,且${F_2}(\sqrt{2},0)$,${F_1}(-\sqrt{2},0)$…(2分)
又|QF1|+|QF2|=3+1=2a.…(4分)
∴a=2,b2=a2-c2=2
∴椭圆C1的方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$.…(6分)
(Ⅱ)当l1平行x轴的时候,l2与圆C2无公共点,从而△MAB不存在;
设l1:x=t(y-1),则l2:tx+y-1=0.
由$\left\{{\begin{array}{l}{\frac{x^2}{4}+\frac{y^2}{2}=1}\\{x=t(y-1)}\end{array}}\right.$,消去x得(t2+2)y2-2t2y+t2-4=0,
则$|AB|=\sqrt{1+{t^2}}|{y_1}-{y_2}|=\frac{{2\sqrt{(1+{t^2})(2{t^2}+8)}}}{{{t^2}+2}}$.…(8分)
又圆心$Q(\sqrt{2},1)$到l2的距离${d_1}=\frac{{|\sqrt{2}t|}}{{\sqrt{1+{t^2}}}}<1$,得t2<1.…(10分)
又MP⊥AB,QM⊥CD
∴M到AB的距离即Q到AB的距离,设为d2,
即${d_2}=\frac{{|\sqrt{2}-t+t|}}{{\sqrt{1+{t^2}}}}=\frac{{\sqrt{2}}}{{\sqrt{1+{t^2}}}}$.…(12分)
∴△MAB面积$S=\frac{1}{2}|AB|•{d_2}=\frac{{2\sqrt{{t^2}+4}}}{{{t^2}+2}}$
令$u=\sqrt{{t^2}+4}∈[2,\sqrt{5})$
则$S=f(u)=\frac{2u}{{{u^2}-2}}=\frac{2}{{u-\frac{2}{u}}}∈(\frac{{2\sqrt{5}}}{3},2]$.
∴△MAB面积的取值范围为$(\frac{{2\sqrt{5}}}{3},2]$.…(15分)
点评 本题考查椭圆方程的求法,考查三角形面积的取值范围的求法,是中档题,解题时要认真审题,注意弦长公式、点到直线距离公式的合理运用.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
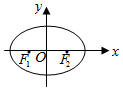 平面直角坐标系xOy中,已知F1、F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且右焦点F2的坐标为($\sqrt{3}$,0),点($\sqrt{3}$,$\frac{1}{2}$)在椭圆C上.
平面直角坐标系xOy中,已知F1、F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且右焦点F2的坐标为($\sqrt{3}$,0),点($\sqrt{3}$,$\frac{1}{2}$)在椭圆C上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
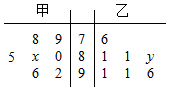 某中学从甲、乙两个艺术班中各选出7名同学参加才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班同学成绩的众数是80,乙班同学成绩的中位数是88,则x+y的值为( )
某中学从甲、乙两个艺术班中各选出7名同学参加才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班同学成绩的众数是80,乙班同学成绩的中位数是88,则x+y的值为( )| A. | 11 | B. | 9 | C. | 8 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | [-1,2] | B. | [0,2] | C. | [-1,$\frac{5}{2}$) | D. | [0,$\frac{5}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com