
分析 由同角三角函数基本关系可得sin(x+$\frac{π}{4}$),进而由二倍角公式可得sin(2x+$\frac{π}{2}$)和cos(2x+$\frac{π}{2}$),再整体代入两角差的余弦公式可得.
解答 解:∵$\frac{17π}{12}$<x<$\frac{7π}{4}$,∴$\frac{5π}{6}$<x+$\frac{π}{4}$<2π,
又∵cos(x+$\frac{π}{4}$)=$\frac{3}{5}$,∴$\frac{3π}{2}$<x+$\frac{π}{4}$<2π,
∴sin(x+$\frac{π}{4}$)=-$\sqrt{1-co{s}^{2}(x+\frac{π}{4})}$=-$\frac{4}{5}$,
∴sin(2x+$\frac{π}{2}$)=2sin(x+$\frac{π}{4}$)cos(x+$\frac{π}{4}$)=-$\frac{24}{25}$,
cos(2x+$\frac{π}{2}$)=cos2(x+$\frac{π}{4}$)-sin2(x+$\frac{π}{4}$)=-$\frac{7}{25}$,
∴cos(2x+$\frac{π}{4}$)=cos[(2x+$\frac{π}{2}$)-$\frac{π}{4}$]
=$\frac{\sqrt{2}}{2}$cos(2x+$\frac{π}{2}$)+$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{2}$)=-$\frac{31\sqrt{2}}{50}$
故答案为:-$\frac{31\sqrt{2}}{50}$
点评 本题考查两角和与差的三角函数公式,涉及二倍角公式和整体思想,属中档题.


科目:高中数学 来源: 题型:解答题
| 高一 | 茎 | 高二 | ||||||||||
| 4 | ||||||||||||
| 3 | 5 | |||||||||||
| 6 | 4 | 2 | 6 | |||||||||
| 6 | 8 | 8 | 6 | 4 | 3 | 7 | ||||||
| 9 | 2 | 8 | 6 | 5 | 1 | 8 | ||||||
| 7 | 5 | 5 | 2 | 9 | ||||||||
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2 | B. | y=x3 | C. | y=x-1 | D. | y=$\sqrt{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
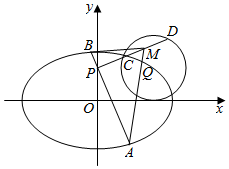 已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F2在以$Q(\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F2在以$Q(\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
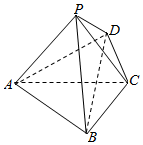 如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,$∠ACB=∠ACD=\frac{π}{3}$
如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,$∠ACB=∠ACD=\frac{π}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
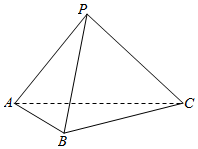 如图,点P是△ABC所在平面外的一点,PA=PB=PC=AB=BC=AC=1,F为AP的中点.
如图,点P是△ABC所在平面外的一点,PA=PB=PC=AB=BC=AC=1,F为AP的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com