
| A. | y=x2 | B. | y=x3 | C. | y=x-1 | D. | y=$\sqrt{x}$ |
分析 求出直线kx-y-2k+4=0恒过定点P的坐标,代人幂函数y=f(x)的解析式,用待定系数法求出f(x)的解析式.
解答 解:直线kx-y-2k+4=0可化为k(x-2)-y+4=0,
令$\left\{\begin{array}{l}{x-2=0}\\{-y+4=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$,
即该直线恒过定点P(2,4);
又幂函数y=f(x)=xa也过点P,
即2a=4,解得a=2;
所以f(x)=x2.
故选:A.
点评 本题考查了求幂函数的解析式,也考查了直线恒过定点的应用问题,是基础题目.


科目:高中数学 来源: 题型:填空题
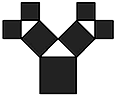 如图所示:一个边长为$\frac{{\sqrt{2}}}{2}$的正方形上连接着等腰直角三角形,等腰直角三角形的边上再连接正方形,…,如此继续.若共得到255个正方形,则最小正方形的边长为$\frac{1}{16}$.
如图所示:一个边长为$\frac{{\sqrt{2}}}{2}$的正方形上连接着等腰直角三角形,等腰直角三角形的边上再连接正方形,…,如此继续.若共得到255个正方形,则最小正方形的边长为$\frac{1}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
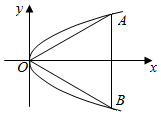 如图,等边三角形OAB的边长为8$\sqrt{3}$,且三个顶点均在抛物线E:y2=2px(p>0)上,O为坐标原点.
如图,等边三角形OAB的边长为8$\sqrt{3}$,且三个顶点均在抛物线E:y2=2px(p>0)上,O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
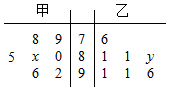 某中学从甲、乙两个艺术班中各选出7名同学参加才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班同学成绩的众数是80,乙班同学成绩的中位数是88,则x+y的值为( )
某中学从甲、乙两个艺术班中各选出7名同学参加才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班同学成绩的众数是80,乙班同学成绩的中位数是88,则x+y的值为( )| A. | 11 | B. | 9 | C. | 8 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a | B. | 0 | C. | -a | D. | 2016 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com