
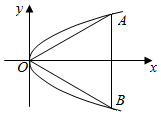
 如图,等边三角形OAB的边长为8$\sqrt{3}$,且三个顶点均在抛物线E:y2=2px(p>0)上,O为坐标原点.
如图,等边三角形OAB的边长为8$\sqrt{3}$,且三个顶点均在抛物线E:y2=2px(p>0)上,O为坐标原点.分析 (Ⅰ)A(x1,y1)、B(x2,y2)根据|OA|=|OB|可得x12+y12=x22+y22.由于A,B都在抛物线上进而满足y12=2px1,y22=2px2,整理可得(x2-x1)(x1+x2+2p)=0.根据x1、x2与p同号可知x1+x2+2p≠0进而可得x1=x2.根据抛物线对称性,知点A、B关于x轴对称.
(Ⅱ)由(Ⅰ)可知∠AOx=30°,进而根据抛物线和直线方程求得点A的坐标,利用等边三角形OAB的边长为8$\sqrt{3}$,可得p,即可求抛物线E的方程.
解答 (Ⅰ)证明:设A(x1,y1)、B(x2,y2),
∵|OA|=|OB|,∴x12+y12=x22+y22.
又∵y12=2px1,y22=2px2,
∴x22-x12+2p(x2-x1)=0,
即(x2-x1)(x1+x2+2p)=0.
又∵x1、x2与p同号,∴x1+x2+2p≠0.
∴x2-x1=0,即x1=x2.
由抛物线对称性,知点A、B关于x轴对称.
(Ⅱ)解:由(Ⅰ)知∠AOx=30°,则y2=2px,x=6p,
∴y=$\frac{\sqrt{3}}{3}$x,y=2$\sqrt{3}$p.
∴A(6p,2$\sqrt{3}$p),
∵等边三角形OAB的边长为8$\sqrt{3}$,
∴(6p)2+(2$\sqrt{3}$p)=(8$\sqrt{3}$)2.
∴p=2,
∴抛物线E的方程为y2=4x.
点评 本题主要考查抛物线的应用和用待定系数法求得曲线方程的问题.是高考中经常考的题目,应加强训练.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 13 | C. | 14 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲、乙的离散程度一样 | B. | 甲的离散程度比乙的离散程度大 | ||
| C. | 乙的离散程度比甲的离散程度大 | D. | 甲、乙的离散程度无法比较 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2 | B. | y=x3 | C. | y=x-1 | D. | y=$\sqrt{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
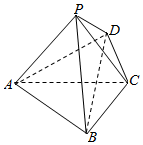 如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,$∠ACB=∠ACD=\frac{π}{3}$
如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,$∠ACB=∠ACD=\frac{π}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份(x) | 2011 | 2012 | 2013 | 2014 | 2015 |
| 家庭数(y) | 6 | 10 | 16 | 22 | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com