
分析 (1)由已知得b=1,e=$\frac{c}{a}=\frac{\sqrt{6}}{3}$,由此能求出椭圆E的方程.
(2)由$\left\{\begin{array}{l}{\frac{{x}^{2}}{3}+{y}^{2}=1}\\{y=kx+\frac{3}{2}}\end{array}\right.$,得$(1+3{k}^{2}){x}^{2}+9kx+\frac{15}{4}$=0,由此利用根的判别式、韦达定理、中点坐标公式、直线垂直的性质,结合已知条件能求出k.
解答 解:(1)∵椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$(a>b>0)的一个顶点为A(0,-1),离心率e=$\frac{\sqrt{6}}{3}$,
∴b=1,e=$\frac{c}{a}=\frac{\sqrt{6}}{3}$,
∵a2=b2+c2,∴c2=2,a2=3,
∴椭圆E的椭圆方程为$\frac{{x}^{2}}{3}+{y}^{2}=1$.
(2)设M(x1,y1),N(x2,y2),则P($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{3}+{y}^{2}=1}\\{y=kx+\frac{3}{2}}\end{array}\right.$,得$(1+3{k}^{2}){x}^{2}+9kx+\frac{15}{4}$=0,
则△=81k2-15(1+3k2)=36k2-15>0,即${k}^{2}>\frac{15}{2}$,①
${x}_{1}+{x}_{2}=-\frac{9k}{1+3{k}^{2}}$,②
∵AP⊥MN,∴kMN•kAP=-1,
即k=$\frac{\frac{{y}_{1}+{y}_{2}}{2}+1}{\frac{{x}_{1}+{x}_{2}}{2}}$=-1,∴k(y1+y2+2)+(x1+x2)=0,
又∵${y}_{1}+{y}_{2}=k{x}_{1}+\frac{3}{2}+k{x}_{2}+\frac{3}{2}$=k(x1+x2)+3,
∴k[k(x1+x2)+5]+(x1+x2)=0,即(k2+1)(x1+x2)+5k=0,③
②代入③,得-(k2+1)•$\frac{9k}{1+3{k}^{2}}$+5k=0,整理,得${k}^{2}=\frac{2}{3}$>$\frac{5}{12}$,满足①,
解得k=±$\frac{\sqrt{6}}{3}$.
点评 本题主要考查直线与圆锥曲线等基础知识,考查运算求解能力、推理论证能力,考查数形结合、化归思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设F1,F2分别是椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,过F1且斜率为1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
设F1,F2分别是椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,过F1且斜率为1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
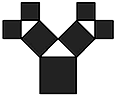 如图所示:一个边长为$\frac{{\sqrt{2}}}{2}$的正方形上连接着等腰直角三角形,等腰直角三角形的边上再连接正方形,…,如此继续.若共得到255个正方形,则最小正方形的边长为$\frac{1}{16}$.
如图所示:一个边长为$\frac{{\sqrt{2}}}{2}$的正方形上连接着等腰直角三角形,等腰直角三角形的边上再连接正方形,…,如此继续.若共得到255个正方形,则最小正方形的边长为$\frac{1}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
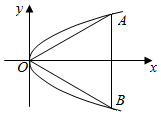 如图,等边三角形OAB的边长为8$\sqrt{3}$,且三个顶点均在抛物线E:y2=2px(p>0)上,O为坐标原点.
如图,等边三角形OAB的边长为8$\sqrt{3}$,且三个顶点均在抛物线E:y2=2px(p>0)上,O为坐标原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com