
分析 (1)令f(m)=2列出方程,转化为二次函数解出;
(2)将函数式子变形,用y表示出x,然后互换变量的符号得出反函数;
(3)先判断反函数的定义域,再计算f-1(-x)+f-1(x).
解答 解:(Ⅰ)由$\frac{{e}^{x}-{e}^{-x}}{2}$=2得:e2m-4em-1=0,解得em=2+$\sqrt{5}$或em=2-$\sqrt{5}$(舍).
∴m=ln(2+$\sqrt{5}$).
(Ⅱ)由y=$\frac{{e}^{x}-{e}^{-x}}{2}$得:e2x-2yex-1=0,解得ex=y+$\sqrt{{y}^{2}+1}$,∴x=ln(y+$\sqrt{{y}^{2}+1}$).
∴f-1(x)=ln(x+$\sqrt{{x}^{2}+1}$)(x∈R).
(Ⅲ)f-1(-x)+f-1(x)=ln(-x+$\sqrt{{x}^{2}+1}$)+ln(x+$\sqrt{{x}^{2}+1}$)=ln1=0.
∴f-1(x)为奇函数.
点评 本题考查了函数值的计算,反函数的求法,函数奇偶性的判断,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2 | B. | y=x3 | C. | y=x-1 | D. | y=$\sqrt{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
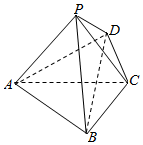 如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,$∠ACB=∠ACD=\frac{π}{3}$
如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,$∠ACB=∠ACD=\frac{π}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份(x) | 2011 | 2012 | 2013 | 2014 | 2015 |
| 家庭数(y) | 6 | 10 | 16 | 22 | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com