
分析 由已知条件,分别求出抛物线的准线方程和双曲线的渐近线,由|AB|=2,求出b=$\frac{\sqrt{3}}{3}$a,由此能求出双曲线的离心率.
解答 解:y2=4$\sqrt{3}$x的准线方程为l:x=-$\sqrt{3}$,
双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线分别为:y=±$\frac{b}{a}$x,
∵抛物线y2=4$\sqrt{3}$x的准线与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1两条渐近线分别交于A,B两点,且|AB|=2,
∴$\frac{2\sqrt{3}b}{a}$=2
即b=$\frac{\sqrt{3}}{3}$a,
∴c=$\frac{2\sqrt{3}}{3}$a,
∴e=$\frac{c}{a}$=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查双曲线的离心率的求法,是中档题,解题时要熟练掌握抛物线、双曲线的简单性质.


科目:高中数学 来源: 题型:解答题
| 做不到科学用眼 | 能做到科学用眼 | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在(0,+∞)上有极大值$\frac{1}{2}$ | B. | f(x)在(0,+∞)上有极小值$\frac{1}{2}$ | ||
| C. | f(x)在(0,+∞)单调递增 | D. | f(x)在(0,+∞)单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
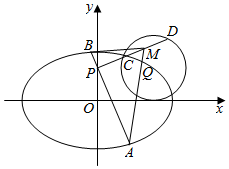 已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F2在以$Q(\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F2在以$Q(\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m⊥n,m∥α,n∥β | B. | m⊥n,α∩β=m,n?α | C. | m∥n,n⊥β,m?α | D. | m∥n,m⊥α,n⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
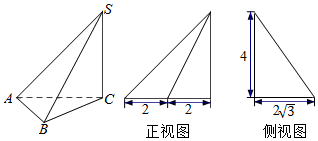
| A. | $16\sqrt{3}$ | B. | $\sqrt{38}$ | C. | $4\sqrt{2}$ | D. | $2\sqrt{11}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com