
分析 (1)由椭圆的离心率为$\frac{\sqrt{3}}{2}$,且点($\sqrt{2}$,$\frac{\sqrt{2}}{2}$)在C上,列出方程组,求出a,b,由此能求出椭圆C的方程.
(2)设直线l的方程为y=k(x-1),与椭圆联立,得$({k}^{2}+\frac{1}{4}){x}^{2}-2{k}^{2}x+{k}^{2}-1=0$,由此利用根的判别式、韦达定理,结合已知条件能求出结果.
解答 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且点($\sqrt{2}$,$\frac{\sqrt{2}}{2}$)在C上,
∴$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{\frac{2}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=1,c=$\sqrt{3}$,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(2)设直线l的方程为y=k(x-1),
联立$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得$({k}^{2}+\frac{1}{4}){x}^{2}-2{k}^{2}x+{k}^{2}-1=0$,
设A(x1,y1),B(x2,y2),则${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{4{k}^{2}+1}$,${x}_{1}{x}_{2}=\frac{4{k}^{2}-4}{4{k}^{2}+1}$,
△>0,
∵$\frac{{d}_{A}}{{d}_{B}}$=$\frac{|PA|}{|PB|}$恒成立,
∴$\frac{{x}_{1}-{x}_{0}}{{x}_{2}-{x}_{0}}$=$\frac{({x}_{1}-1)\sqrt{1+{k}^{2}}}{(1-{x}_{2})\sqrt{1+{k}^{2}}}$,
∴2x1x2-(1+x0)(x1+x2)+2x0=0,
将x1+x2与x1x2的值代入得2x0-8=0,
解得x0=4.
∴存在直线l0:x=x0(其中x0>2),使A,B到l0的距离dA,dB满足:$\frac{{d}_{A}}{{d}_{B}}$=$\frac{|PA|}{|PB|}$恒成立,且x0的值为4.
点评 本题考查椭圆方程的求法,考查满足条件的直线是否存在的判断与求法,是中档题,解题时要认真审题,注意椭圆性质、根的判别式、韦达定理的合理运用.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
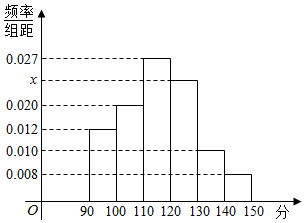 某校高一年级为组建数学兴趣小组,对参加报名的100名同进行了摸底考试,发现其成绩都在90-150分之间.频率分布直方图如图所示
某校高一年级为组建数学兴趣小组,对参加报名的100名同进行了摸底考试,发现其成绩都在90-150分之间.频率分布直方图如图所示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com