
| A. | 0 | B. | 1 | C. | -1 | D. | $\sqrt{2}$ |
分析 根据题意,将a、b的值代入ab中可得,ab=$\frac{1-co{s}^{2}α}{si{n}^{2}α}$=$\frac{si{n}^{2}α}{si{n}^{2}α}$,化简可得答案.
解答 解:根据题意,a=$\frac{1-cosα}{sinα}$,b=$\frac{1+cosα}{sinα}$,
则ab=$\frac{1-cosα}{sinα}$×$\frac{1+cosα}{sinα}$=$\frac{(1-cosα)(1+cosα)}{si{n}^{2}α}$=$\frac{1-co{s}^{2}α}{si{n}^{2}α}$=$\frac{si{n}^{2}α}{si{n}^{2}α}$=1;
故选:B.
点评 本题考查同角三角函数基本关系式的运用,关键是掌握同角三角函数基本关系式并灵活运用.


科目:高中数学 来源: 题型:选择题
| A. | m⊥n,m∥α,n∥β | B. | m⊥n,α∩β=m,n?α | C. | m∥n,n⊥β,m?α | D. | m∥n,m⊥α,n⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
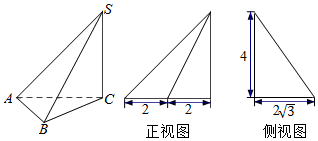
| A. | $16\sqrt{3}$ | B. | $\sqrt{38}$ | C. | $4\sqrt{2}$ | D. | $2\sqrt{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
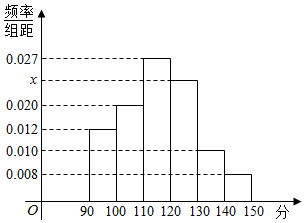 某校高一年级为组建数学兴趣小组,对参加报名的100名同进行了摸底考试,发现其成绩都在90-150分之间.频率分布直方图如图所示
某校高一年级为组建数学兴趣小组,对参加报名的100名同进行了摸底考试,发现其成绩都在90-150分之间.频率分布直方图如图所示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | -32 | C. | 48 | D. | -48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com