Question

18．（1）如果角a的终边在第二象限．讨论$\frac{a}{2}$的终边所在的位置．
（2）由此可否得出更一般的结论？并画出a的终边在第一、二、三、四象限时．$\frac{a}{2}$的终边所在的位置．
（3）类似地讨论$\frac{a}{3}$的位置（可设a在第一象限．讨论$\frac{a}{3}$终边的位置．井推广到一般情形）．

Answer 1

分析 （1）写出第二象限角的范围，可得$\frac{a}{2}$的终边所在的位置；
（2）直接由（1）的结论推广得到a的终边在第一、二、三、四象限时，$\frac{a}{2}$的终边所在的位置，并画出图形；
（3）由a在第一象限，讨论得到$\frac{a}{3}$终边的位置并进一步推广到一般情形．

解答 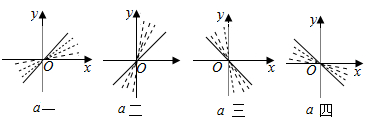解：（1）由角a的终边在第二象限，得$\frac{π}{2}+2kπ＜a＜π+2kπ，k∈Z$，
则$\frac{π}{4}+kπ＜\frac{a}{2}＜\frac{π}{2}+kπ，k∈Z$，
当k为奇数时，$\frac{a}{2}$的终边在第三象限，当k为偶数时，$\frac{a}{2}$的终边在第一象限；
（2）由（1）可得，当a的终边在第一、二、三、四象限时，
$\frac{a}{2}$的终边分别在第一或第三、第一或第三、第二或第四、第二第四象限；
如图：
（3）当a的终边在第一象限时，即$2kπ＜a＜\frac{π}{2}+2kπ$，得$\frac{2}{3}kπ＜\frac{a}{3}＜\frac{π}{6}+\frac{2kπ}{3}，k∈Z$，
∴$\frac{a}{3}$的终边在第一或第二或第三象限；
推广可知：当a的终边在第二象限时，$\frac{a}{3}$的终边在第一或第二或第四象限；
当a的终边在第三象限时，$\frac{a}{3}$的终边在第一或第三或第四象限；
当a的终边在第四象限时，$\frac{a}{3}$的终边在第二或第三或第四象限．

点评 本题考查象限角和轴线角，考查集合思想方法的应用，是中档题．