下列命题正确的是( )
A.命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0”
B.设回归直线方程为y=2-2.5x,当变量x增加一个单位时,y平均增加2个单位
C.已知ξ服从正态分布N(0,O-2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=0.2
D.若向量a,b满足a•b<0,则a与b的夹角为钝角.
【答案】
分析:根据逆否命题的定义,写出其逆否命题,判断A是否正确;
根据回归分析基本思想判断B是否正确;
根据正态分布的对称性判断C是否正确;
根据向量的数量积公式判断D是否正确.
解答:解:根据逆否命题的定义,“若x
2+y
2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x
2+y
2≠0”,∴A正确;
对B选项,当变量x增加一个单位时,y平均减少2.5个单位,∴B错误;
根据正态分布的对称性,P(ξ>2)=P(ξ<-2)=

×(1-2×0.4)=0.1,∴C错误;
∵当
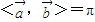
时,
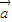
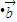
<0,∴D错误.
故选A
点评:本题借助考查命题的真假判断,考查回归分析基本思想、正态分布及向量的夹角等知识.

 ×(1-2×0.4)=0.1,∴C错误;
×(1-2×0.4)=0.1,∴C错误;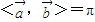 时,
时,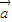
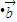 <0,∴D错误.
<0,∴D错误.
