
【题目】已知函数 ![]() ,g(x)=x+lnx,其中a>0.
,g(x)=x+lnx,其中a>0.
(1)若x=1是函数h(x)=f(x)+g(x)的极值点,求实数a的值;
(2)若对任意的x1 , x2∈[1,e](e为自然对数的底数)都有f(x1)≥g(x2)成立,求实数a的取值范围.
【答案】
(1)解:∵ ![]() ,g(x)=x+lnx,
,g(x)=x+lnx,
∴ ![]() ,其定义域为(0,+∞),
,其定义域为(0,+∞),
∴ ![]() .
.
∵x=1是函数h(x)的极值点,
∴h′(1)=0,即3﹣a2=0.
∵a>0,∴ ![]()
经检验当 ![]() 时,x=1是函数h(x)的极值点,
时,x=1是函数h(x)的极值点,
∴ ![]()
(2)解:对任意的x1,x2∈[1,e]都有f(x1)≥g(x2)成立等价于
对任意的x1,x2∈[1,e]都有[f(x)]min≥[g(x)]max.
当x∈[1,e]时, ![]() .
.
∴函数g(x)=x+lnx在[1,e]上是增函数.
∴[g(x)]max=g(e)=e+1.
∵ ![]() ,且x∈[1,e],a>0.
,且x∈[1,e],a>0.
①当0<a<1且x∈[1,e]时, ![]() ,
,
∴函数 ![]() 在[1,e]上是增函数,
在[1,e]上是增函数,
∴ ![]() .
.
由1+a2≥e+1,得a≥ ![]() ,
,
又0<a<1,∴a不合题意;
②当1≤a≤e时,
若1≤x<a,则 ![]() ,
,
若a<x≤e,则 ![]() .
.
∴函数 ![]() 在[1,a)上是减函数,在(a,e]上是增函数.
在[1,a)上是减函数,在(a,e]上是增函数.
∴[f(x)]min=f(a)=2a.
由2a≥e+1,得a≥ ![]() ,
,
又1≤a≤e,∴ ![]() ≤a≤e;
≤a≤e;
③当a>e且x∈[1,e]时, ![]() ,
,
∴函数 ![]() 在[1,e]上是减函数.
在[1,e]上是减函数.
∴ ![]() .
.
由 ![]() ≥e+1,得a≥
≥e+1,得a≥ ![]() ,
,
又a>e,∴a>e;
综上所述:a的取值范围为 ![]()
【解析】(1)通过 ![]() 、x=1是函数h(x)的极值点及a>0,可得
、x=1是函数h(x)的极值点及a>0,可得 ![]() ,再检验即可; (2)通过分析已知条件等价于对任意的x1 , x2∈[1,e]都有[f(x)]min≥[g(x)]max . 结合当x∈[1,e]时及
,再检验即可; (2)通过分析已知条件等价于对任意的x1 , x2∈[1,e]都有[f(x)]min≥[g(x)]max . 结合当x∈[1,e]时及 ![]() 可知[g(x)]max=g(e)=e+1.利用
可知[g(x)]max=g(e)=e+1.利用 ![]() ,且x∈[1,e],a>0,分0<a<1、1≤a≤e、a>e三种情况讨论即可.
,且x∈[1,e],a>0,分0<a<1、1≤a≤e、a>e三种情况讨论即可.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.a>b是ac2>bc2的充要条件
B.a>1,b>1是ab>1的充分条件
C.?x0∈R,e ![]() ≤0
≤0
D.若p∨q为真命题,则p∧q为真
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为
短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的一个焦点
的一个焦点![]() 重合,直线
重合,直线![]() 与抛物线
与抛物线![]() 交于两点
交于两点![]() ,且
,且![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为
短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的一个焦点
的一个焦点![]() 重合,直线
重合,直线![]() 与抛物线
与抛物线![]() 交于两点
交于两点![]() ,且
,且![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点. (Ⅰ)求证:直线AF∥平面PEC;
(Ⅱ)求PC与平面PAB所成角的正弦值.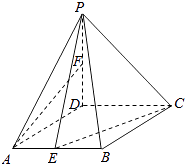
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两个研发小组,他们研发新产品成功的概率分别为 ![]() 和
和 ![]() .现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立. (Ⅰ)求至少有一种新产品研发成功的概率;
.现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立. (Ⅰ)求至少有一种新产品研发成功的概率;
(Ⅱ)若新产品A研发成功,预计企业可获利润120万元;若新产品B研发成功,预计企业可获利润100万元,求该企业可获利润的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com