
【题目】已知椭圆![]() 短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为
短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的一个焦点
的一个焦点![]() 重合,直线
重合,直线![]() 与抛物线
与抛物线![]() 交于两点
交于两点![]() ,且
,且![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)先写出一个短轴端点与一个焦点的直线方程可以是![]() ,即
,即![]() ,利用圆心到直线距离等于半径,列方程求解即可;
,利用圆心到直线距离等于半径,列方程求解即可;
(2)抛物线![]() 的焦点在
的焦点在![]() 轴的正半轴上,故
轴的正半轴上,故![]() ,故
,故![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() ,由
,由![]() ,可得
,可得![]() ,设点
,设点![]() ,则
,则![]() ,
, ![]() 代入求出关于
代入求出关于![]() 的表达式,利用判别式大于0
的表达式,利用判别式大于0![]() 的范围,求值域即可.
的范围,求值域即可.
试题解析:
(1) 设椭圆的焦距为![]() ,则由条件可得
,则由条件可得![]() ,连接一个短轴端点与一个焦点的直线方程可以是
,连接一个短轴端点与一个焦点的直线方程可以是![]() ,即
,即![]() ,由直线与圆相切可得
,由直线与圆相切可得![]() ,故
,故![]() ,则
,则![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() .
.
(2) 抛物线![]() 的焦点在
的焦点在![]() 轴的正半轴上,故
轴的正半轴上,故![]() ,故
,故![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() ,由
,由![]() ,可得
,可得![]() ,由直线
,由直线![]() 与抛物线
与抛物线![]() 有两个不同交点可得
有两个不同交点可得
![]() 在
在![]() 时恒成立,设点
时恒成立,设点![]() ,则
,则![]() ,则
,则![]() ,又点
,又点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,故
,故![]() 的面积为
的面积为![]() .令
.令![]() ,则
,则![]() ,令
,令![]() ,可得
,可得![]() 或
或![]() ,故
,故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,故
上单调递减,故![]() 时,
时, ![]() 取最大值
取最大值![]() ,则
,则![]() 的面积取最大值为
的面积取最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】(12分)在数列![]() 中,对于任意
中,对于任意![]() ,等式
,等式![]()
成立,其中常数![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求证:数列![]() 为等比数列;
为等比数列;
(Ⅲ)如果关于n的不等式![]() 的解集为
的解集为
![]() ,求b和c的取值范围.
,求b和c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 |
|
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) |
| 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55] | 15 | 0.3 |
(1)补全频率分布直方图并求![]() 的值;
的值;
(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.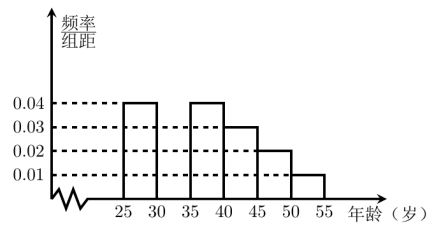
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于95为正品,小于95为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为正品的概率;
(2)甲机床生产一件零件,若是正品可盈利160元,次品则亏损20元;乙机床生产一件零件,若是正品可盈利200元,次品则亏损40元,在(1)的前提下,现需生产这种零件2件,以获得利润的期望值为决策依据,应该如何安排生产最佳?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为4的正方形![]() 的边上有一点
的边上有一点![]() 沿着折线
沿着折线![]() 由点
由点![]() (起点)向点
(起点)向点![]() (终点)运动。设点
(终点)运动。设点![]() 运动的路程为
运动的路程为![]() ,
,![]() 的面积为
的面积为![]() ,且
,且![]() 与
与![]() 之间的函数关系式用如图所示的程序框图给出.
之间的函数关系式用如图所示的程序框图给出.
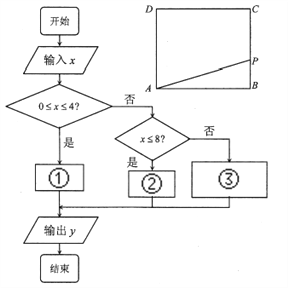
(1)写出框图中①、②、③处应填充的式子;
(2)若输出的面积![]() 值为6,则路程
值为6,则路程![]() 的值为多少?并指出此时点
的值为多少?并指出此时点![]() 在正方形的什么位置上?
在正方形的什么位置上?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6 ,
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an , 求数列{ ![]() }的前n项和.
}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.
(1)求AD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子原件生产厂生产的10件产品中,有8件一级品,2件二级品,一级品和二级品在外观上没有区别.从这10件产品中任意抽检2件,计算:
(1)2件都是一级品的概率;
(2)至少有一件二级品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com