
【题目】在边长为4的正方形![]() 的边上有一点
的边上有一点![]() 沿着折线
沿着折线![]() 由点
由点![]() (起点)向点
(起点)向点![]() (终点)运动。设点
(终点)运动。设点![]() 运动的路程为
运动的路程为![]() ,
,![]() 的面积为
的面积为![]() ,且
,且![]() 与
与![]() 之间的函数关系式用如图所示的程序框图给出.
之间的函数关系式用如图所示的程序框图给出.
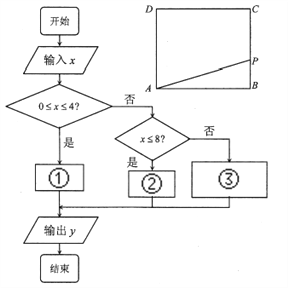
(1)写出框图中①、②、③处应填充的式子;
(2)若输出的面积![]() 值为6,则路程
值为6,则路程![]() 的值为多少?并指出此时点
的值为多少?并指出此时点![]() 在正方形的什么位置上?
在正方形的什么位置上?
【答案】(1)![]() ;(2)当
;(2)当![]() 时,点
时,点![]() 在正方形的
在正方形的![]() 上;当
上;当![]() 时,点
时,点![]() 在正方形的
在正方形的![]() 上.
上.
【解析】试题分析:(1)先求出定义域,然后根据点P的位置进行分类讨论,根据三角形的面积公式求出每一段△ABP的面积与P移动的路程间的函数关系式,最后用分段函数进行表示即可写出框图中①、②、③处应填充的式子;(2)利用△APB的面积为6,结合函数解析式,建立等式,即可求x的取值,进而得出此时点P的在正方形的什么位置上
试题解析:(1)由于x=0与x=12时,三点A、B、P不能构成三角形,故这个函数的
定义域为(0,12).
当0<x≤4时,S=f(x)=![]() 4x=2x;
4x=2x;
当4<x≤8时,S=f(x)=8;
当8<x<12时,S=f(x)=![]() 4(12﹣x)=2(12﹣x)=24﹣2x.
4(12﹣x)=2(12﹣x)=24﹣2x.
∴这个函数的解析式为f(x)=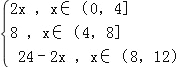 ,
,
∴框图中①、②、③处应填充的式子分别为:y=2x,y=8,y=24﹣2x.
(2)若输出的面积y值为6,则
当0<x≤4时,2x=6,∴x=3;
当8<x<12时,S=24﹣2x=6,∴x=9,
综上,当x=3时,此时点P的在正方形的边BC上,当x=9时,此时点P的在正方形的边DA上.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosC+(cosA﹣![]() sinA)cosB=0.
sinA)cosB=0.
(1)求角B的大小; (2)若a+c=1,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x|x﹣a|(其中a∈R).
(1)当a=1时,求函数f(x)的值域;
(2)若y=f(x)在[0,2]上的最小值为﹣1,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出y关于x的回归方程;
(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中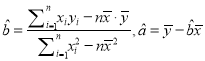 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为
短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的一个焦点
的一个焦点![]() 重合,直线
重合,直线![]() 与抛物线
与抛物线![]() 交于两点
交于两点![]() ,且
,且![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩(均为整数)分成六段![]() 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:

(1)求第四小组的频率,并补全频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是![]() ~
~![]() 分及
分及![]() ~
~![]() 分的学生中选两人,记他们的成绩为
分的学生中选两人,记他们的成绩为![]() ,求满足“
,求满足“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),以坐标原点为极点,
),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)讨论直线![]() 与圆
与圆![]() 的公共点个数;
的公共点个数;
(Ⅱ)过极点作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,求点
,求点![]() 的轨迹与圆
的轨迹与圆![]() 相交所得弦长.
相交所得弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从![]() 个招标问题中随机抽取
个招标问题中随机抽取![]() 个问题,已知这
个问题,已知这![]() 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的![]() 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为![]() ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲、乙两家公司共答对![]() 道题目的概率;
道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点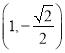 是椭圆
是椭圆![]() 上的点,离心率
上的点,离心率![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 在椭圆
在椭圆![]() 上,若点
上,若点![]() 与点
与点![]() 关于原点对称,连接
关于原点对称,连接![]() 并延长与椭圆
并延长与椭圆![]() 的另一个交点为
的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com