
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点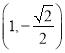 是椭圆
是椭圆![]() 上的点,离心率
上的点,离心率![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 在椭圆
在椭圆![]() 上,若点
上,若点![]() 与点
与点![]() 关于原点对称,连接
关于原点对称,连接![]() 并延长与椭圆
并延长与椭圆![]() 的另一个交点为
的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据条件列出关于![]() 两个方程,解方程组可得
两个方程,解方程组可得![]() 值,即得椭圆
值,即得椭圆![]() 的方程;(2)联立直线方程与椭圆方程,利用韦达定理及弦长公式可得底边长
的方程;(2)联立直线方程与椭圆方程,利用韦达定理及弦长公式可得底边长![]() (用直线斜率表示),根据点到直线距离公式可得三角形的高(用直线斜率表示),根据三角形面积公式可得
(用直线斜率表示),根据点到直线距离公式可得三角形的高(用直线斜率表示),根据三角形面积公式可得![]() 面积,关于直线斜率的函数关系式,最后根据分式函数求值域方法求函数最值,注意讨论斜率不存在的情形.
面积,关于直线斜率的函数关系式,最后根据分式函数求值域方法求函数最值,注意讨论斜率不存在的情形.
试题解析:(1)依题意,![]() ,
,![]() ,
,![]() ,解得
,解得![]() 。
。
故椭圆![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 的斜率不存在时,不妨取
的斜率不存在时,不妨取![]() ,
,
故![]() .
.
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
联立方程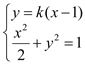 化简得
化简得![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
因为![]() 是线段
是线段![]() 的中点,所以点
的中点,所以点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴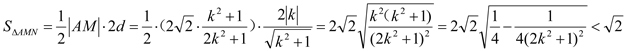 .
.
综上,![]() 面积的最大值为
面积的最大值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】在边长为4的正方形![]() 的边上有一点
的边上有一点![]() 沿着折线
沿着折线![]() 由点
由点![]() (起点)向点
(起点)向点![]() (终点)运动。设点
(终点)运动。设点![]() 运动的路程为
运动的路程为![]() ,
,![]() 的面积为
的面积为![]() ,且
,且![]() 与
与![]() 之间的函数关系式用如图所示的程序框图给出.
之间的函数关系式用如图所示的程序框图给出.
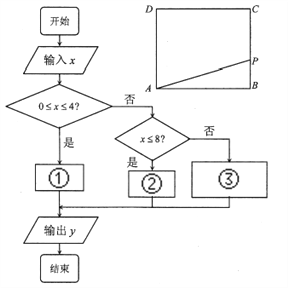
(1)写出框图中①、②、③处应填充的式子;
(2)若输出的面积![]() 值为6,则路程
值为6,则路程![]() 的值为多少?并指出此时点
的值为多少?并指出此时点![]() 在正方形的什么位置上?
在正方形的什么位置上?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四凌锥S﹣ABCD中,底面ABCD是直角梯形,AD∥BC,SA⊥CD,AB⊥平面SAD,M是SC的中点,且SA=AB=BC=2,AD=1. 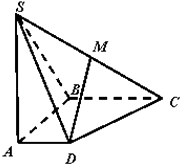
(1)求证:DM∥平面SAB;
(2)求四棱锥S﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
, ![]() ,
, ![]() ,
, ![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品获奖情况预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品获奖情况预测如下:
甲说:“![]() 或
或![]() 作品获得一等奖”
作品获得一等奖”
乙说:“![]() 作品获得一等奖”
作品获得一等奖”
丙说:“![]() ,
, ![]() 两项作品未获得一等奖”
两项作品未获得一等奖”
丁说:“![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子原件生产厂生产的10件产品中,有8件一级品,2件二级品,一级品和二级品在外观上没有区别.从这10件产品中任意抽检2件,计算:
(1)2件都是一级品的概率;
(2)至少有一件二级品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B分别是直线y=x和y=﹣x上的两个动点,线段AB的长为2 ![]() ,D是AB的中点.
,D是AB的中点.
(1)求动点D的轨迹C的方程;
(2)若过点(1,0)的直线l与曲线C交于不同两点P、Q,
①当|PQ|=3时,求直线l的方程;
②试问在x轴上是否存在点E(m,0),使 ![]()
![]() 恒为定值?若存在,求出E点的坐标及定值;若不存在,请说明理由.
恒为定值?若存在,求出E点的坐标及定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,an=32,sn=63,
(1)若数列{an}为公差为11的等差数列,求a1;
(2)若数列{an}为以a1=1为首项的等比数列,求数列{am2}的前m项和sm′ .
查看答案和解析>>
科目:高中数学 来源: 题型:
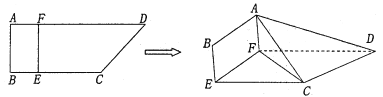
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别在
分别在![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使
折起,使![]() .
.
(1)若![]() ,在折叠后的线段
,在折叠后的线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(2)求三棱锥![]() 的体积的最大值,并求出此时点
的体积的最大值,并求出此时点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知E、F分别在正方体ABCD﹣A1B1C1D1的棱BB1、CC1上,且B1E=2EB,CF=2FC1 , 则面AEF与面ABC所成的二面角的正切值等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com