
某商品每件成本5元,售价14元,每星期卖出75件.如果降低价格,销售量可以增加,且每星期多卖出的商品件数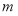 与商品单价的降低值
与商品单价的降低值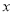 (单位:元,
(单位:元,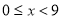 )的平方成正比,已知商品单价降低1元时,一星期多卖出5件.
)的平方成正比,已知商品单价降低1元时,一星期多卖出5件.
(1)将一星期的商品销售利润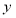 表示成
表示成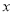 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
(1)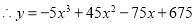
 ;(2)当
;(2)当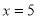 即商品每件定价为9元时,可使一个星期的商品销售利润最大
即商品每件定价为9元时,可使一个星期的商品销售利润最大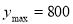 .
.
【解析】
试题分析:(1)先写出多卖的商品数,则可计算出商品在一个星期的获利数,再依题意:“商品单价降低1元时,一星期多卖出5件”求出比例系数,即可得一个星期的商品销售利润表示成 的函数;(2)根据(1)中得到的函数,利用导数研究其极值,也就是求出函数的极大值,从而得出定价为多少元时,能使一个星期的商品销售利润最大.
的函数;(2)根据(1)中得到的函数,利用导数研究其极值,也就是求出函数的极大值,从而得出定价为多少元时,能使一个星期的商品销售利润最大.
试题解析:(1)依题意,设 ,由已知有
,由已知有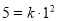 ,从而
,从而
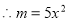 3分
3分

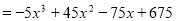
 7分
7分
(2) 9分
9分
由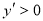 得
得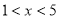 ,由
,由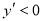 得
得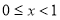 或
或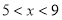
可知函数 在
在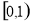 上递减,在
上递减,在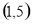 递增,在
递增,在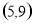 上递减 11分
上递减 11分
从而函数 取得最大值的可能位置为
取得最大值的可能位置为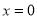 或是
或是
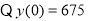 ,
,
 当
当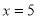 时,
时,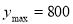 13分
13分
答:商品每件定价为9元时,可使一个星期的商品销售利润最大 14分.
考点:1.函数模型及其应用;2.导数的实际应用.


科目:高中数学 来源:2015届广东阳东广雅、阳春实验中学高二上期末文数学卷(解析版) 题型:选择题
已知x>0,则y=3x+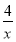 有( )
有( )
A.最大值4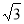 B.最小值4
B.最小值4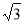 C.最大值2
C.最大值2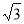 D.最小值2
D.最小值2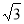
查看答案和解析>>
科目:高中数学 来源:2015届广东汕头金山中学高二上学期期末文科数学试卷(解析版) 题型:选择题
下列说法中,错误的个数是( )
①一条直线与一个点就能确定一个平面
②若直线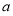 ∥
∥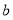 ,
,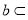 平面
平面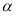 ,则
,则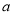 ∥
∥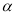
③若函数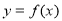 定义域内存在
定义域内存在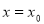 满足
满足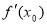
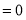 ,则
,则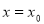 必定是
必定是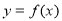 的极值点
的极值点
④函数的极大值就是最大值
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2015届广东台山高二第一学期期末测试理科数学试卷(解析版) 题型:选择题
甲、乙两人同时从图书馆走向教室,甲一半路程步行,一半路程跑步;乙一半时间步行,一半时间跑步,若两人步行、跑步的速度一样,则先到教室的是
A.甲 B.乙 C.甲、乙同时到达 D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com