
是否存在常数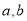 ,使等式
,使等式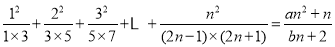 对于一切
对于一切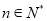 都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
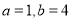 ,证明详见解析.
,证明详见解析.
【解析】
试题分析:先从特殊情形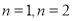 ,等式必须成立,求出
,等式必须成立,求出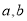 值,然后用数学归纳法加以证明,在这里必须指出的是:若题目没有讲要用数学归纳法证明,我们也应从数学归纳法考虑,因为等式的左边我们无法通过数列求和的知识解决,其次本题是与自然数有关的命题证明,我们应优先考虑数学归纳法,证明时必须严格遵循数学归纳法的证题步骤,做到规范化.
值,然后用数学归纳法加以证明,在这里必须指出的是:若题目没有讲要用数学归纳法证明,我们也应从数学归纳法考虑,因为等式的左边我们无法通过数列求和的知识解决,其次本题是与自然数有关的命题证明,我们应优先考虑数学归纳法,证明时必须严格遵循数学归纳法的证题步骤,做到规范化.
试题解析:若存在常数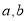 使等式成立,则将
使等式成立,则将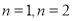 代入上式,有
代入上式,有 得
得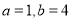 ,即有
,即有 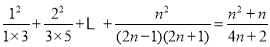 对于一切
对于一切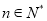 成立. 5分
成立. 5分
数学归纳法证明如下:
证明如下:(1)当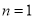 时,左边=
时,左边=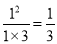 ,右边=
,右边=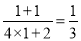 ,所以等式成立,
,所以等式成立,
(2)假设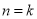 (
(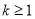 且
且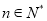 )时等式成立,即
)时等式成立,即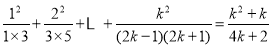 ,
,
当 时,
时,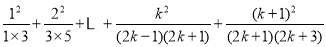
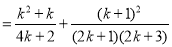
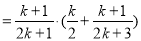
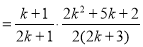
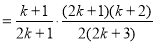

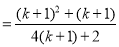
也就是说,当 时,等式成立,
时,等式成立,
综上所述,可知等式对任何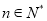 都成立. 12分
都成立. 12分
考点:数学归纳法.


科目:高中数学 来源:2015届湖北省武汉市高三9月调考理科数学试卷(解析版) 题型:选择题
已知变量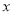 与
与 正相关,且由观测数据算得样本平均数
正相关,且由观测数据算得样本平均数 ,
,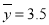 ,则由该观测数据算得的线性回归方程可能是( )
,则由该观测数据算得的线性回归方程可能是( )
A.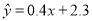 B.
B.
C.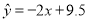 D.
D.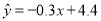
查看答案和解析>>
科目:高中数学 来源:2015届湖北省武汉市高三9月调考文科数学试卷(解析版) 题型:选择题
小王从甲地到乙地往返的时速分别为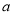 和
和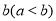 ,其全程的平均时速为
,其全程的平均时速为 ,则( )
,则( )
A. B.
B.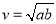 C.
C.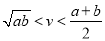 D.
D.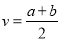
查看答案和解析>>
科目:高中数学 来源:2015届湖北省咸宁市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
已知函数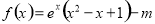 ,若
,若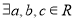 ,且
,且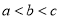 ,使得
,使得 .则实数
.则实数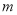 的取值范围是( )
的取值范围是( )
A.(﹣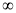 ,1) B.(1,
,1) B.(1,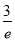 )
)
C.(1,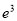 ) D.(﹣
) D.(﹣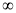 ,1)∪(
,1)∪(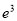 ,+
,+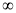 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com