
设命题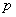 :对任意实数
:对任意实数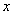 ,不等式
,不等式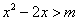 恒成立;命题
恒成立;命题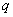 :方程
:方程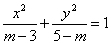 表示焦点在
表示焦点在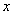 轴上的双曲线.
轴上的双曲线.
(1)若命题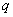 为真命题,求实数
为真命题,求实数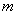 的取值范围;
的取值范围;
(2)若命题“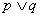 ”为真命题,且“
”为真命题,且“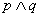 ”为假命题,求实数
”为假命题,求实数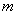 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
若椭圆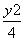 +
+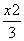 =1的两个焦点F1,F2,M是椭圆上一点,且|MF1|-|MF2|=1,则△MF1F2是( )
=1的两个焦点F1,F2,M是椭圆上一点,且|MF1|-|MF2|=1,则△MF1F2是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆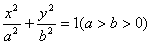 的长轴长为
的长轴长为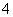 ,离心率为
,离心率为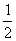 ,
,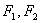 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点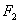 ,且与直线
,且与直线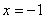 相切。
相切。
(Ⅰ) (ⅰ)求椭圆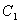 的方程; (ⅱ)求动圆圆心轨迹
的方程; (ⅱ)求动圆圆心轨迹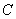 的方程;
的方程;
(Ⅱ) 在曲线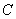 上有两点
上有两点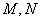 ,椭圆
,椭圆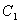 上有两点
上有两点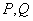 ,满足
,满足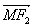 与
与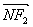 共线,
共线,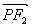 与
与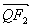 共线,且
共线,且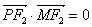 ,求四边形
,求四边形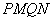 面积的最小值。
面积的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
为了调查任教班级的作业完成的情况,将班级里的52名学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知5号、31号、44号同学在样本中,那么样本中还有一位同学的编号应该是( ).
A.13 B.17 C.18 D.21
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=mx3+nx2(m、n∈R ,m≠0)的图像在(2,f(2))处的切线与x轴平行.
(1)求n,m的关系式并求f(x)的单调减区间;
(2)证明:对任意实数0<x1<x2<1, 关于x的方程:
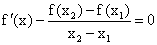 在(x1,x2)恒有实数解
在(x1,x2)恒有实数解
(3)结合(2)的结论,其实我们有拉格朗日中值定理:若函数f(x)是在闭区间[a,b]上连续不断的函数,且在区间(a,b)内导数都存在,则在(a,b)内至少存在一点x0,使得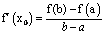 .如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
.如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
当0<a<b时,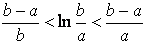 (可不用证明函数的连续性和可导性)
(可不用证明函数的连续性和可导性)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com