
【题目】如图所示,在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.
(Ⅰ)若BM=2MP,求证:PD∥平面MAC;
(Ⅱ)若平面PAB⊥平面ABCD,平面PAD⊥平面ABCD,求证:PA⊥平面ABCD;
(Ⅲ)在(Ⅱ)的条件下,若二面角B﹣AC﹣M的余弦值为 ![]() ,求
,求 ![]() 的值.
的值.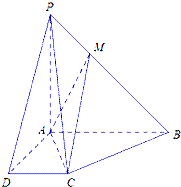
【答案】证明:(Ⅰ)连结BD交AC于点O,连结OM.
因为 AB∥CD,AB=2CD,所以 ![]() .
.
因为 BM=2MP,所以 ![]() .所以
.所以 ![]() .
.
所以OM∥PD.
因为 OM平面MAC,PD平面MAC,
所以 PD∥平面MAC.
(Ⅱ)因为 平面PAD⊥平面ABCD,AD⊥AB,
平面PAD∩平面ABCD=AD,AB平面ABCD,
所以AB⊥平面PAD.
因为PA平面PAD,所以AB⊥PA.
同理可证:AD⊥PA.
因为 AD平面ABCD,AB平面ABCD,AD∩AB=A,
所以PA⊥平面ABCD.
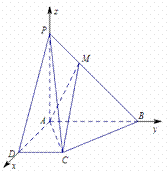
解:(Ⅲ)分别以边AD,AB,AP所在直线为x,y,z轴,
建立如图所示的空间直角坐标系.
由AB=AD=AP=2CD=2,
得A(0,0,0),B(0,2,0),C(2,1,0),D(2,0,0),P(0,0,2),
则 ![]() ,
, ![]() .
.
由(Ⅱ)得:PA⊥平面ABCD.
所以 平面ABCD的一个法向量为 ![]() .
.
设 ![]() (0≤λ≤1),即
(0≤λ≤1),即 ![]() .所以
.所以 ![]() .
.
设平面AMC的法向量为 ![]() ,
,
则 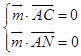 ,即
,即 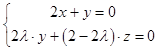
令x=λ﹣1,则y=2﹣2λ,z=﹣2λ.所以 ![]() .
.
因为 二面角B﹣AC﹣M的余弦值为 ![]() ,
,
所以 ![]() ,解得
,解得 ![]() .
.
所以 ![]() 的值为
的值为 ![]() .
.

【解析】(Ⅰ)连结BD交AC于点O,连结OM,推导出OM∥PD,由此能证明PD∥平面MAC.(Ⅱ)推导出AB⊥PA,AD⊥PA,由此能证明PA⊥平面ABCD.(Ⅲ)分别以边AD,AB,AP所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出 ![]() 的值.
的值.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对平面与平面垂直的判定的理解,了解一个平面过另一个平面的垂线,则这两个平面垂直.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABO﹣A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1 , OB=3,O1B1=1,OO1= ![]() .
. 
(1)证明:AB1⊥BO1;
(2)求直线AO1与平面AOB1所成的角的正切值;
(3)求二面角O﹣AB1﹣O1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=e|lnx|(e为自然对数的底数).若x1≠x2且f(x1)=f(x2),则下列结论一定不成立的是( )
A.x2f(x1)>1
B.x2f(x1)=1
C.x2f(x1)<1
D.x2f(x1)<x1f(x2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,下列结论中错误的是
,下列结论中错误的是
A. ![]()
![]() , f(
, f(![]() )=0
)=0
B. 函数y=f(x)的图像是中心对称图形
C. 若![]() 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞,![]() )单调递减
)单调递减
D. 若![]() 是f(x)的极值点,则
是f(x)的极值点,则![]() (
(![]() )=0
)=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ![]() ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点. 
(1)求证AM∥平面BDE;
(2)求二面角A﹣DF﹣B的大小;
(3)试在线段AC上一点P,使得PF与CD所成的角是60°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=﹣an﹣( ![]() )n﹣1+2(n∈N*),数列{bn}满足bn=2nan .
)n﹣1+2(n∈N*),数列{bn}满足bn=2nan .
(Ⅰ)求证数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)设cn=log2 ![]() ,数列{
,数列{ ![]() }的前n项和为Tn , 求满足Tn
}的前n项和为Tn , 求满足Tn ![]() (n∈N*)的n的最大值.
(n∈N*)的n的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com