
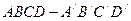 中
中
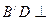 平面
平面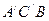 ;
;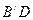 与平面
与平面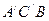 的交点
的交点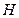 是
是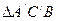 的重心(三角形三条中线的交点)
的重心(三角形三条中线的交点)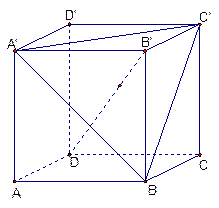 |
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 平面ABEF,如图所示,FD
平面ABEF,如图所示,FD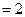 , AD=1, EF=
, AD=1, EF=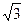 .
.
 平面FCB;
平面FCB;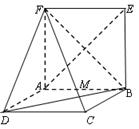
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
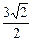
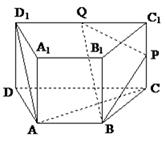
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
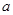 升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点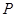 (图2)。有下列四个命题:
(图2)。有下列四个命题:| A.正四棱锥的高等于正四棱柱高的一半 |
B.将容器侧面水平放置时,水面也恰好过点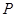 |
C.任意摆放该容器,当水面静止时,水面都恰好经过点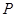 |
D.若往容器内再注入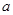 升水,则容器恰好能装满 升水,则容器恰好能装满 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
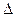 BCD的三条高线的交点;
BCD的三条高线的交点;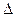 ABC和
ABC和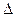 ABD的边AB上的高,则这两条高所在直线异面;
ABD的边AB上的高,则这两条高所在直线异面;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
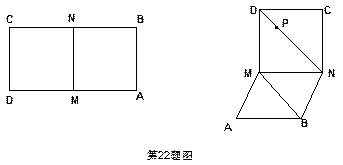
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com