
分析 (1)列举出所有的满足条件的事件,根据古典概型概率公式得到结果;
(2)a∈(-5,2),b∈(0,4),图象如图所示的矩形部分,其面积为28,满足△=4(a-2)2-4b2<0.a∈(-5,2),b∈(0,4),图象如图所示的阴影部分,其面积为8,由此能求出方程有实根的概率.
解答 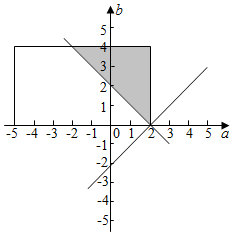 解:(1)一元二次方程x2+2(a-2)x+b2=0的△=4(a-2)2-4b2≥0.
解:(1)一元二次方程x2+2(a-2)x+b2=0的△=4(a-2)2-4b2≥0.
a∈(-5,2)且a∈Z,b∈(0,4)且b∈Z,基本事件有(-4,1),(-4,2),(-4,3),(-3,1),(-3,2),(-3,3),(-2,1),(-2,2),(-2,3),
(-1,1),(-1,2),(-1,3),(0,1),(0,2),(0,3),(1,1),(1,2),(1,3),共18个,
满足方程有实根的基本事件有(-4,1),(-4,2),(-4,3),(-3,1),(-3,2),(-3,3),(-2,1),(-2,2),(-2,3),(-1,1),(-1,2),
(-1,3),(0,1),(0,2),(1,1),共15个,
∴方程有实根的概率为$\frac{15}{18}$=$\frac{5}{6}$;
(2)a∈(-5,2),b∈(0,4),图象如图所示的矩形部分,其面积为28,
满足△=4(a-2)2-4b2<0.a∈(-5,2),b∈(0,4),图象如图所示的阴影部分,其面积为8,∴方程无实根的概率.为$\frac{8}{28}$=$\frac{2}{7}$.
点评 高中必修中学习了几何概型和古典概型两种概率问题,解题时,先要判断该概率模型是不是古典概型,再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.再看是不是几何概型,它的结果要通过长度、面积或体积之比来得到.


科目:高中数学 来源: 题型:选择题
| A. | (7,-2) | B. | (6,-2) | C. | (-1,6) | D. | (-2,7) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com