
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
分析 (1)利用平均数公式计算即得.
(2)把所给的7对数据写成对应的点的坐标,在坐标系中描出来,得到散点图.
(3)作出利用最小二乘法来求线性回归方程的系数的量,求出横标和纵标的平均数,求出系数,再求出a的值,即可求出回归方程.
(4)x=9时,y=4.75×9+51.36≈94.1,即可求出相应于点(9,91)的残差.
解答 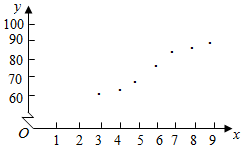 解:(1)$\overline{x}$=$\frac{1}{7}$(3+4+5+6+7+8+9)=6,$\overline{y}$=$\frac{1}{7}$(66+69+73+81+89+90+91)=$\frac{559}{7}$≈79.86;(4分)
解:(1)$\overline{x}$=$\frac{1}{7}$(3+4+5+6+7+8+9)=6,$\overline{y}$=$\frac{1}{7}$(66+69+73+81+89+90+91)=$\frac{559}{7}$≈79.86;(4分)
(2)把所给的7对数据写成对应的点的坐标,在坐标系中描出来,得到散点图; (2分)
(3)由散点图知,y与x有线性相关关系,(2分)
3×66+4×69+5×73+6×81+7×89+8×90+9×91=3487,32+42+52+62+72+82+92=280,
∴b=$\frac{3487-7×6×\frac{559}{7}}{280-7×36}$=4.75,(3分)
a=79.86-6×4.75=51.36.(1分)
∴回归直线方程y=4.75x+51.36.(1分)
(4)x=9时,y=4.75×9+51.36≈94.1
相应于点(9,91)的残差91-94.1=-3.1(12分)
点评 本题考查线性回归方程的求法和应用,本题解题的关键是利用最小二乘法做出线性回归方程的系数,本题是一个近几年可能出现在高考卷中的题目.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
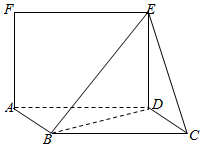 如图,平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,正方形ADEF,且面ADEF⊥面ABCD.
如图,平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,正方形ADEF,且面ADEF⊥面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4.
如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (-∞,-2)∪(2,+∞) | C. | (2,+∞) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com