
分析 设g(x)=x|x-a|,由题意可以得到g(x)min≥a-$\frac{3}{2}$,分1≤a≤2或a>2,讨论即可求出a的取值范围.
解答 解:∵x|x-a|$+\frac{3}{2}$≥a对任意x∈[1,2]恒成立,
即x|x-a|≥a-$\frac{3}{2}$恒成立,
设g(x)=x|x-a|,在x∈[1,2]恒成立有g(x)≥a-$\frac{3}{2}$,
∴g(x)min=a-$\frac{3}{2}$,
当1≤a≤2时,g(x)=x|x-a|=$\left\{\begin{array}{l}{x(x-a),a≤x<2}\\{x(a-x),1≤x<a}\end{array}\right.$
故g(x)在[1,2]上的最小值为g(a)=0,
即0≥a-$\frac{3}{2}$,解得1≤a≤$\frac{3}{2}$,
当a>2时,g(x)=x(a-x),g(x)在x∈[1,2]恒成立有
g(x)≥a-$\frac{3}{2}$,
故$\left\{\begin{array}{l}{g(1)≥a-\frac{3}{2}}\\{g(2)≥a-\frac{3}{2}}\end{array}\right.$,即$\left\{\begin{array}{l}{a-1≥a-\frac{3}{2}}\\{2(a-2)≥a-\frac{3}{2}}\end{array}\right.$,
解得a≥$\frac{5}{2}$
综上所述a的取值范围为[1,$\frac{3}{2}$]∪[$\frac{5}{2}$,+∞).
点评 本题考查带绝对值的函数,考查函数恒成立问题,突出考查转化思想与分类讨论思想、方程思想的综合应用应用,考查逻辑思维能力与运算能力,属于难题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患心肺疾病 | 不患心肺疾病 | 合计 | |
| 大于40岁 | 16 | ||
| 小于或等于40岁 | 12 | ||
| 合计 | 80 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
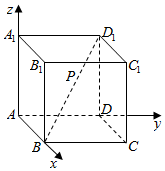 在如图的空间直角坐标系中,正方体ABCD-A1B1C1D1的棱长为1,P是线段BD1上的一点,且BP=2PD1,则点P的坐标是( )
在如图的空间直角坐标系中,正方体ABCD-A1B1C1D1的棱长为1,P是线段BD1上的一点,且BP=2PD1,则点P的坐标是( )| A. | ($\frac{1}{3}$,$\frac{2}{3}$,$\frac{2}{3}$) | B. | ($\frac{2}{3}$,$\frac{1}{3}$,$\frac{2}{3}$) | C. | ($\frac{2}{3}$,$\frac{2}{3}$,$\frac{2}{3}$) | D. | ($\frac{1}{3}$,$\frac{1}{3}$,$\frac{2}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com