练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    有下列四个游戏盘，如果撒一粒黄豆落在阴影部分，则可中奖．小明希望中奖，他应当选择的游戏盘为(　　)


     A


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设f(x)，g(x)分别是定义在R上的奇函数和偶函数，当x<0时，f′(x)g(x)＋f(x)g′(x)>0，且g(－3)＝0，则不等式f(x)g(x)<0的解集是________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b，c∈R，函数f(x)＝ax2＋bx＋c.若f(0)＝f(4)＞f(1)，则(　　)

    A．a＞0,4a＋b＝0       B．a＜0,4a＋b＝0

    C．a＞0,2a＋b＝0       D．a＜0,2a＋b＝0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝a·2x＋b·3x，其中常数a，b满足ab≠0.

    (1)若ab>0，判断函数f(x)的单调性；

    (2)若ab<0，求f(x＋1)>f(x)时x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)由下表给出，

    x

    1

    2

    3

    f(x)

    2

    3

    1

    　则f(f(2))＝______，满足f(f(x))>f(3)的x的值是______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


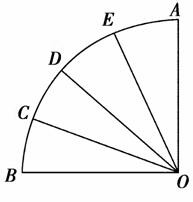
    扇形AOB的半径为1，圆心角为90°.点C，D，E将弧AB等分成四份．连接OC，OD，OE，从图中所有的扇形中随机取出一个，面积恰为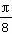的概率是(　　)

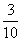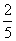    A.         B.         C.        D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有这样的算法：

    第一步，设i的值为1.

    第二步，设sum的值为0.

    第三步，若i≤100，执行第四步，否则转去执行第七步．

    第四步，计算sum＋(i＋1)/i，并将结果代替sum.

    第五步，计算i＋1，并将结果代替i.

    第六步，转去执行第三步．

    第七步，输出sum的值，并结束算法．

    这个算法是　(　　)

    A．求2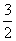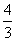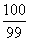＋＋＋…＋的和

    B．求2＋＋＋…＋的和

    C．求1＋＋＋…＋的和

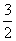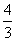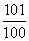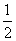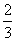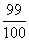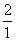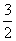
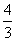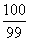    D．求1＋＋＋＋…＋的和

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    甲、乙两人下棋，和棋的概率为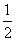，乙获胜的概率为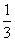，则下列说法正确的是(　　)

    A．甲获胜的概率是        B．甲不输的概率是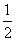

    C．乙输了的概率是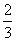        D．乙不输的概率是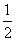

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某地区为了解70～80岁老人的日平均睡眠时间(单位：h)，随机选择了50位老人进行调查．下表是这50位老人日睡眠时间的频率分布表.

    序号

    (i)

    分组

    (睡眠时间)

    组中值

    (Gi)

    频数

    (人数)

    频率

    (Fi)

    1

    [4,5)

    4.5

    6

    0.12

    2

    [5,6)

    5.5

    10

    0.20

    3

    [6,7)

    6.5

    20

    0.40

    4

    [7,8)

    7.5

    10

    0.20

    5

    [8,9)

    8.5

    4

    0.08

    在上述统计数据的分析中，一部分计算见算法流程图(注：符号“←”与“＝”的含义相同)，则输出的S的值是________．

    查看答案和解析>>

    同步练习册答案