已知数列{an},{bn}满足a1=2,a2=4,bn=an+1-an,bn+1=2bn+2.
(1)求证:数列{bn+2}是公比为2的等比数列; (2)求an.
解:(1)由
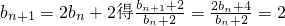
,
∴{b
n+2}是公比为2的等比数列.
(2)由(1)可知b
n+2=4•2
n-1=2
n+1.∴b
n=2
n+1-2.则a
n+1-a
n=2
n+1-2
令n=1,2,…n-1,则a
2-a
1=2
2-2,a
3-a
2=2
3-2,…a
n-a
n-1=2
n-2,
各式相加得a
n=(2+2
2+2
3+…+2
n)-2(n-1)=2
n+1-2-2n+2=2
n+1-2n.
所以a
n=2
n+1-2n.
分析:(1)利用b
n+1=2b
n+2.构造数列{b
n+2},通过等比数列的定义,证明数列是等比数列.
(2)利用(1)求出数列b
n=2
n+1-2.通过b
n=a
n+1-a
n,推出数列a
n的递推关系式,利用累加法求出数列的通项公式即可.
点评:本题是中档题,考查数列的证明,数列的递推关系式的应用,通项公式的求法,考查计算能力,逻辑推理能力.

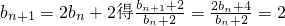 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案