
平面内动点P到点F(1,0)的距离等于它到直线x=-1的距离,记点P的轨迹为曲线Γ.
(1)求曲线Γ的方程;
(2)若点A,B,C是Γ上的不同三点,且满足 +
+ +
+ =0,证明:△ABC不可能为直角三角形.
=0,证明:△ABC不可能为直角三角形.
(1)y2=4x(2)不可能是直角三角形
【解析】(1)由条件可知,点P到点F(1,0)的距离与到直线x=-1的距离相等,所以点P的轨迹是以F(1,0)为焦点,x=-1为准线的抛物线,其方程为y2=4x.
(2)证明:方法一,假设△ABC是直角三角形,且∠A=90°,
A(x1,y1),B(x2,y2),C(x3,y3),则
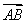 =(x2-x1,y2-y1),
=(x2-x1,y2-y1),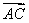 =(x3-x1,y3-y1),且
=(x3-x1,y3-y1),且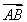 ·
·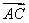 =0,
=0,
所以(x2-x1)(x3-x1)+(y2-y1)(y3-y1)=0.
因为xi=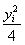 (i=1,2,3),y1≠y2,y1≠y3,
(i=1,2,3),y1≠y2,y1≠y3,
所以(y1+y2)(y1+y3)+16=0.
又因为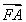 +
+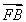 +
+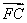 =0,所以x1+x2+x3=3,y1+y2+y3=0,
=0,所以x1+x2+x3=3,y1+y2+y3=0,
所以y2y3=-16,①
又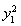 +
+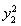 +
+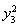 =4(x1+x2+x3)=12,
=4(x1+x2+x3)=12,
所以(-y2-y3)2+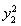 +
+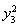 =12,即
=12,即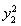 +
+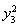 +y2y3=6,②
+y2y3=6,②
由①②得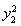 +
+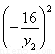 -16=6,即
-16=6,即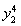 -22
-22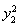 +256=0,③
+256=0,③
因为Δ=(-22)2-4×256=-540<0.
所以方程③无解,从而△ABC不可能是直角三角形.
方法二,设A(x1,y1),B(x2,y2),C(x3,y3),由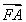 +
+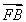 +
+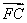 =0,
=0,
得x1+x2+x3=3,y1+y2+y3=0.欲证△ABC不是直角三角形,只需证明∠A≠90°.
(ⅰ)当AB⊥x轴时,x1=x2,y1=-y2,从而x3=3-2x1,y3=0,
即点C的坐标为(3-2x1,0).
由于点C在y2=4x上,所以3-2x1=0,即x1=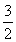 ,
,
此时A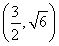 ,B
,B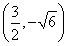 ,C(0,0),则∠A≠90°.
,C(0,0),则∠A≠90°.
(ⅱ)当AB与x轴不垂直时,设直线AB的方程为x=ty+m(t≠0),代入y2=4x,整理得y2-4ty-4m=0,则y1+y2=4t.
若∠A=90°,则直线AC的斜率为-t,同理可得y1+y3=-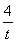 .
.
由y1+y2+y3=0,得y1=4t-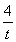 ,y2=
,y2=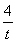 ,y3=-4t.
,y3=-4t.
由x1+x2+x3=3,可得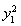 +
+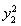 +
+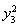 =4(x1+x2+x3)=12.
=4(x1+x2+x3)=12.
从而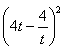 +
+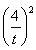 +(-4t)2=12,
+(-4t)2=12,
整理得t2+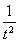 =
=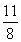 ,即8t4-11t2+8=0,④
,即8t4-11t2+8=0,④
Δ=(-11)2-4×8×8=-135<0.
所以方程④无解,从而∠A≠90°.
综合(ⅰ)(ⅱ)可知,△ABC不可能是直角三角形.


科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:选择题
已知e为自然对数的底数,则函数y=xex的单调递增区间是( )
A.[-1,+∞) B.(-∞,-1]
C.[1,+∞) D.(-∞,1]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第1课时练习卷(解析版) 题型:填空题
设命题p:?a>0,a≠1,函数f(x)=ax-x-a有零点.则?p: ________________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(解析版) 题型:填空题
在数列{an}中,a1=1,a2=2,若当整数n>1时,Sn+1+Sn-1=2(Sn+S1)恒成立,则S15=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(解析版) 题型:选择题
已知{an}为等差数列,若a3+a4+a8=9,则S9=( )
A.24 B.27 C.15 D.54
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题六练习卷(解析版) 题型:填空题
已知等差数列{an}的首项为a1,公差为d,其前n项和为Sn,若直线y=a1x与圆(x-2)2+y2=4的两个交点关于直线x+y+d=0对称,则Sn=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题六练习卷(解析版) 题型:选择题
若抛物线y2=2px的焦点与双曲线 =1的右焦点重合,则p的值为( )
=1的右焦点重合,则p的值为( )
A.-2 B.2 C.-4 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题八练习卷(解析版) 题型:选择题
已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)等于( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题三练习卷(解析版) 题型:选择题
若ω>0,函数y=cosωx+ 的图像向右平移
的图像向右平移 个单位长度后与原图像重合,则ω的最小值为( )
个单位长度后与原图像重合,则ω的最小值为( )
A.  B.
B.  C.3 D.4
C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com