
���� ��1�����ü������ֱ������Ĺ�ϵ��������CΪ��ͨ���̣����ֱ�߷��̣��������߷��̣��ⷽ�̿ɵý������꣬��ת��Ϊ�����ꣻ
��2�������ҳ���ʽ�͵㵽ֱ�ߵľ��빫ʽ�����ֱ�ߵ�б�ʹ�ʽ���ɵ���б�ǣ�
��� �⣺��1������C�ļ����귽��Ϊ��-4sin��=0����Ϊ��
��2=4��sin�ȣ�����x2+y2-4y=0��
����=$\frac{3��}{4}$ʱ��ֱ�ߵ�б��Ϊ-1��ֱ��l�ķ���Ϊy-4=-x��
����ֱ�߷��̺�Բ�ķ��̣��ɵ�$\left\{\begin{array}{l}{x=0}\\{y=4}\end{array}\right.$��$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$��
��Ӧ�ļ�����Ϊ��4��$\frac{��}{2}$������2$\sqrt{2}$��$\frac{��}{4}$����
��2���ɣ�1������C��ʾԲ��Ϊ��0��2�����뾶Ϊ2��Բ��
���ҳ���ʽ�ɵ�2$\sqrt{3}$=2$\sqrt{4-{d}^{2}}$��
���d=1��
��ֱ��AB�ķ���Ϊy-4=kx����k=tan������
����d=$\frac{|0-2+4|}{\sqrt{1+{k}^{2}}}$=1�����k=��$\sqrt{3}$��
��ֱ��l����б��Ϊ$\frac{��}{3}$��$\frac{2��}{3}$��
���� ���⿼��������̡������귽������ͨ���̵Ļ���������ֱ�ߺ�Բ��λ�ù�ϵ���Լ��ҳ���ʽ�����ã������е��⣮


 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-4��+�ޣ� | B�� | ��-�ޣ�-1���ȣ�3��+�ޣ� | C�� | ��-�ޣ�-1]��[3��+�ޣ� | D�� | ��-4��-1]��[3��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
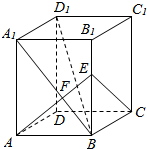 ��ͼ����֪��������ABCD-A1B1C1D1 �ĵ���߳�Ϊ3�����ⳤΪ4������A1B����A��AF��A1B����ΪF����AF���ӳ��߽�B1B��E��
��ͼ����֪��������ABCD-A1B1C1D1 �ĵ���߳�Ϊ3�����ⳤΪ4������A1B����A��AF��A1B����ΪF����AF���ӳ��߽�B1B��E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
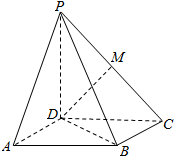 ��ͼ��������P-ABCD�У�����ABCDΪ�����Σ�PD��ƽ��ABCD��M��PC���е㣮
��ͼ��������P-ABCD�У�����ABCDΪ�����Σ�PD��ƽ��ABCD��M��PC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{2}$ | B�� | 2 | C�� | $\sqrt{3}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com