
已知函数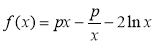 .
.
(1)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若函数 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
(3)设函数 ,若在
,若在 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1) ;(2)
;(2)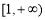 ;(3)
;(3)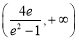 .
.
【解析】
试题分析:本题主要考查导数的运算、利用导数求曲线的切线、利用导数判断函数的单调性、利用导数求函数的最值、恒成立问题等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力,考查学生的分类讨论思想、函数思想.第一问,对 求导,将切点的横坐标代入得到切线的斜率,再将切点的横坐标代入到
求导,将切点的横坐标代入得到切线的斜率,再将切点的横坐标代入到 中,得到切点的纵坐标,利用点斜式得到切线的方程;第二问,
中,得到切点的纵坐标,利用点斜式得到切线的方程;第二问, 在定义域
在定义域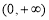 内是增函数,只需
内是增函数,只需 在
在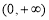 恒成立,对
恒成立,对 求导,由于分母恒正,只需分子
求导,由于分母恒正,只需分子 在
在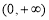 恒成立,设函数
恒成立,设函数 ,利用抛物线的性质求出
,利用抛物线的性质求出 ,令
,令 即可,解出P的值;第三问,先通过函数
即可,解出P的值;第三问,先通过函数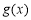 的单调性求出
的单调性求出 的值域,通过对P的讨论研究
的值域,通过对P的讨论研究 的单调性,求出
的单调性,求出 的值域,看是否有值大于
的值域,看是否有值大于 的最小值为2.
的最小值为2.
(1)当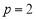 时,函数
时,函数 ,
, .
.
 ,曲线
,曲线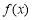 在点
在点 处的切线的斜率为
处的切线的斜率为 .
.
从而曲线 在点
在点 处的切线方程为
处的切线方程为 ,即
,即 .…4分
.…4分
(2) .
.
令 ,要使
,要使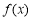 在定义域
在定义域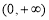 内是增函数,只需
内是增函数,只需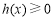 在
在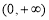 内恒成立.
内恒成立.
由题意 ,
, 的图象为开口向上的抛物线,对称轴方程为
的图象为开口向上的抛物线,对称轴方程为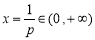 ,∴
,∴ , 只需
, 只需 ,即
,即 时,
时,
∴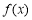 在
在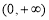 内为增函数,正实数
内为增函数,正实数 的取值范围是
的取值范围是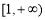 .……9分
.……9分
(3)∵ 在
在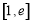 上是减函数,
上是减函数,
∴ 时,
时, ;
; 时,
时, ,即
,即 ,
,
①当 时,
时, ,其图象为开口向下的抛物线,对称轴
,其图象为开口向下的抛物线,对称轴 在
在 轴的左侧,且
轴的左侧,且 ,所以
,所以 在
在
 内是减函数.
内是减函数.
当 时,
时, ,因为
,因为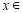
 ,所以
,所以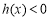 ,
,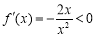 ,
,
此时, 在
在
 内是减函数.
内是减函数.
故当 时,
时,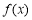 在
在 上单调递减
上单调递减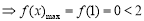 ,不合题意;
,不合题意;
②当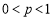 时,由
时,由 ,所以
,所以 .
.
又由(2)知当 时,
时, 在
在 上是增函数,
上是增函数,
∴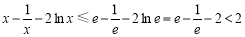 ,不合题意;
,不合题意;
③当 时,由(2)知
时,由(2)知 在
在 上是增函数,
上是增函数, ,
,
又 在
在 上是减函数,故只需
上是减函数,故只需 ,
, ,
,
而 ,
, ,
,
即 ,解得
,解得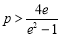 ,
,
所以实数 的取值范围是
的取值范围是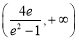 . 14分
. 14分
考点:导数的运算、利用导数求曲线的切线、利用导数判断函数的单调性、利用导数求函数的最值、恒成立问题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源:2013-2014学年陕西省高考第七次适应性训练理科数学试卷(解析版) 题型:选择题
平面上有一组平行线且相邻平行线间的距离为 ,把一枚半径为
,把一枚半径为 的硬币任意平掷在这个平面,则硬币不与任何一条平行线相碰的概率是( )
的硬币任意平掷在这个平面,则硬币不与任何一条平行线相碰的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高考第七次适应性训练文科数学试卷(解析版) 题型:填空题
已知如下算法语句
输入t;
If t<5 Then y=t2+1;
Else if t<8 Then y=2t-1;
Else y= ;
;
End If
End if
输出y
若输入t=8,则下列程序执行后输出的结果是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高考第七次适应性训练文科数学试卷(解析版) 题型:选择题
已知 的三顶点坐标为
的三顶点坐标为 ,
, ,
, ,
, 点的坐标为
点的坐标为 ,向
,向 内部投一点
内部投一点 ,那么点
,那么点 落在
落在 内的概率为( ).
内的概率为( ).
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高三下学期第八次适应性训练理科数学试卷(解析版) 题型:解答题
设函数 .
.
(1)求 的值域;
的值域;
(2)记 的内角
的内角 的对边长分别为
的对边长分别为 ,若
,若 ,
, ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高三第六次模拟理科数学试卷(解析版) 题型:填空题
A.(坐标系与参数方程)已知直线的参数方程为 (为参数),圆
(为参数),圆 的参数方程为
的参数方程为 (
( 为参数), 则圆心
为参数), 则圆心 到直线的距离为_________.
到直线的距离为_________.
B.(几何证明选讲)如右图,直线 与圆
与圆 相切于点
相切于点 ,割线
,割线
 经过圆心
经过圆心 ,弦
,弦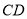 ⊥
⊥ 于点
于点 ,
,  ,
, ,则
,则 _________.
_________.
C.(不等式选讲)若存在实数 使
使 成立,则实数
成立,则实数
的取值范围是_________.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年重庆市高三下学期考前模拟(二诊)理科数学试卷(解析版) 题型:解答题
已知向量 ,函数
,函数 的最小正周期为
的最小正周期为 .
.
(1)求 的值;
的值;
(2)设 的三边
的三边 、
、 、
、 满足:
满足: ,且边
,且边 所对的角为
所对的角为 ,若关于
,若关于 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com