
����Ŀ��Ŀǰ����������Ϊһ�߿�űҩƷ�õ������ƹ�ijũ����Ϊ�������о��������ض������ز�����Ӱ�죬��ɽ�Ϻ�ɽ�µ��������зֱ���ֲ��![]() ��������жԱ�����.���ڴ�ɽ�Ϻ�ɽ�µ��������и����ѡȡ��
��������жԱ�����.���ڴ�ɽ�Ϻ�ɽ�µ��������и����ѡȡ��![]() ��������Ϊ������ÿ����ȡ�������ز�������λ���ˣ����±���ʾ��
��������Ϊ������ÿ����ȡ�������ز�������λ���ˣ����±���ʾ��
���� | �� | �� | �� | �� |
ɽ�� |
|
|
|
|
ɽ�� |
|
|
|
|
��1�������������ݣ��Թ���ɽ�������������ص��ܲ�����
��2����ɽ����ɽ�����������ﵥ�������ز����ķ���ֱ�Ϊ![]() ��
��![]() �������������ݣ��Թ���
�������������ݣ��Թ���![]() ��
��![]() �Ĵ�С��ϵ��ֻ��д�����ۣ���
�Ĵ�С��ϵ��ֻ��д�����ۣ���
��3���������е�ɽ����ɽ�������и����ѡȡ![]() �꣬����
�꣬����![]() ��IJ����ܺ�Ϊ
��IJ����ܺ�Ϊ![]() �ĸ���.
�ĸ���.
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() .
.
��������
��1����ɽ��������![]() ���������������ز������ݣ����������ƽ������ɽ��������
���������������ز������ݣ����������ƽ������ɽ��������![]() ������������ز���
������������ز���![]() �Ĺ���ֵ��
�Ĺ���ֵ��
��2���Ƚ�ɽ�ϡ�ɽ�µ����������������ز������ݵ���ɢ�̶ȣ��ɵó�![]() ��
��![]() �Ĵ�С��ϵ��
�Ĵ�С��ϵ��
��3�����¼�![]() ���г�����ó���ɽ����ɽ�������и����ѡȡ
���г�����ó���ɽ����ɽ�������и����ѡȡ![]() ��������ز����ܺͣ��ӱ����еó������¼������������ó��¼�
��������ز����ܺͣ��ӱ����еó������¼������������ó��¼�![]() �������Ļ����¼��������ùŵ���͵ĸ��ʹ�ʽ�ɼ�����¼�
�������Ļ����¼��������ùŵ���͵ĸ��ʹ�ʽ�ɼ�����¼�![]() �ĸ���.
�ĸ���.
��1����ɽ��������![]() ���������������ز������ݣ�������ƽ����
���������������ز������ݣ�������ƽ����![]() ��
��
��ɽ��������![]() ������������ص��ܲ���
������������ص��ܲ���![]() ����Ϊ��
������![]() ��
��
��2����������ɽ�ϡ�ɽ�µ��������ز�������ɢ�̶�֪![]() ��
��
��3����![]() Ϊ�¼�
Ϊ�¼�![]() ���б���
�����
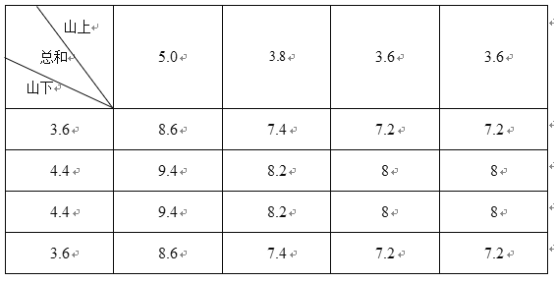
���ϱ����Կ�������![]() ��IJ����ܺ�
��IJ����ܺ�![]() �������������
�������������![]() �֣�
�֣�
������![]() ���������
���������![]() �֣��ʣ�
�֣��ʣ�![]() .
.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ��
��![]() �ϵ�����������ʵ��
�ϵ�����������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ʱ����֤�����������
ʱ����֤�����������![]() ������
������![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017�߿��¿α������19����ͼ��������ABCD�У���ABC���������Σ���ACD��ֱ�������Σ���ABD=��CBD��AB=BD��
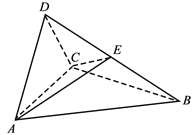
��1��֤����ƽ��ACD��ƽ��ABC��
��2����AC��ƽ�潻BD�ڵ�E����ƽ��AEC��������ABCD�ֳ������ȵ������֣�������D�CAE�CC������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ɽ��ʡ�߿��ĸ��Ե㷽�����涨����2017���^������ѧ��������ʼ�����������ƣ�2020�꿪ʼ���߿��ܳɼ���������3��ͳ����Ŀ����������ѧ������ѡ����Ŀ����.��ÿ��ѡ����Ŀ�Ŀ���ԭʼ�ɼ��Ӹߵ��ͻ���ΪA��B+��B��C+��C��D+��D��E��8���ȼ�.������̬�ֲ�ԭ��ȷ�����ȼ�������ռ�����ֱ�Ϊ3%��7%��16%��24%��24%��16%��7%��3%.ѡ����Ŀ�ɼ����뿼���ܳɼ�ʱ����A��E�ȼ��ڵĿ���ԭʼ�ɼ������յȱ���ת�����ֱ�ת����[91,100]��[81,90]��[71,80]��[61,70]��[51,60]��[41,50]��[31,40]��[21,30]�˸��������䣬�õ������ĵȼ��ɼ���
ijУ��һ�꼶��2000�ˣ�Ϊ����һѧ������ѡ���ṩ���ݣ�������ѡ����Ŀ���в��ԣ�������������ԭʼ�ɼ�����������̬�ֲ�N��60,169����
����������ԭʼ�ɼ������䣨47,86����������
�����߿��ĸ﷽��������ȫʡ�����������ȡ3�ˣ���X��ʾ��3���еȼ��ɼ�������[61,80]����������X�ķֲ��к���ѧ����.
���������������![]() ����
����![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������![]() �У��ı���
�У��ı���![]() Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ�![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() .
.

��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() ��ֱ��
��ֱ��![]() ���ɽ�
���ɽ�![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����Ϊ�˽⡰���š�ÿ���ܲ���ƽ����̣��ռ���������2018��1����2018��11���ڼ䡰���š�ÿ���ܲ���ƽ����̣���λ����������ݣ����������������ͼ.��������ͼ�����н�����ȷ���ǣ� ��

A. ���ܲ�ƽ����̵���λ��Ϊ6�·ݶ�Ӧ�������
B. ���ܲ�ƽ�������������
C. ���ܲ�ƽ����̸߷��ڴ�����8��9��
D. 1����5�µ����ܲ�ƽ����������6����11�£������Ը�С���仯�Ƚ�ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ʽ��������ѧ�ҿ������о���ѧ�����еġ�����������ʱ�õ��ģ�������ʷ�ĽǶȽ����ò���ʽӦ����Ϊ�������������ǿƷ�˹������ʩ�ߴIJ���ʽ����Ϊ���Ǻ���λ��ѧ�ұ˴˶������ڻ���ѧ���ƶ���֮���Ž���һ����ʽ�ƹ㵽���Ƶĵز����ڸ�����ѧѡ�̲�4��5�и����˶�ά��ʽ�Ŀ�������ʽ����a2+b2����c2+d2������ac+bd��2���ҽ���ad��bc����![]() ��ʱ�Ⱥų������ò���ʽ����ѧ��֤������ʽ��������ֵ�ȷ��涼�й㷺��Ӧ�ã����ݿ�������ʽ��֪����
��ʱ�Ⱥų������ò���ʽ����ѧ��֤������ʽ��������ֵ�ȷ��涼�й㷺��Ӧ�ã����ݿ�������ʽ��֪����![]() �����ֵ��ȡ�����ֵʱx��ֵ�ֱ�Ϊ��������
�����ֵ��ȡ�����ֵʱx��ֵ�ֱ�Ϊ��������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ֳƾ��ɰ壬�����������ɰ������ƴͼ.�ഫ�Ǽ�����ײ��������ĵ���ƴͼ�������и��ײ�����ƴͼһ��.��ͼ�����ɰ���2���������ı��Ρ�2���������Ρ�1��С�����Ρ�2�������������κ�����С�������.��ƴͼʱ����ʹ���������������߿������ӣ�����������ص�.���ɰ���ƴ�ڳ�һ�ٶ��ַ���ͼ�Σ���˵�DZ仯�������Ȥζ�����Ҳ����Ϊ��������ƴ��.��֪ƴͼ�������������Σ�ͼ����Ӱ���֣�Ϊֱ�DZ߳�Ϊ2�ĵ���ֱ�������Σ��������ģ��ķ���������˾��ɰ�������������ھ��ɰ���ѡȡ100���㣬������34���������������������ڣ���˾��ɰ�������ԼΪ______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
(1)����![]() �ĵ�����;
�ĵ�����;
(2)��![]() ��ʾ
��ʾ![]() �е����ֵ��������
�е����ֵ��������![]() ֻ��һ�����,��
ֻ��һ�����,��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com