
 ,AB=BC=2AD=4,E、F分别是AB、CD上的中点,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的中点,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图).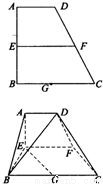
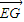 与
与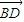 的数量积为零即可;
的数量积为零即可;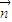 1,然后求出法向量为
1,然后求出法向量为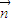 1与
1与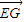 的夹角,根据EG和平面ABCD所成的角与法向量为
的夹角,根据EG和平面ABCD所成的角与法向量为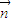 1与
1与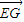 的夹角互补即可求得;
的夹角互补即可求得; 2,利用两平面的法向量求出两向量的夹角的余弦值,从而得到二面角B-DC-F的余弦值.
2,利用两平面的法向量求出两向量的夹角的余弦值,从而得到二面角B-DC-F的余弦值.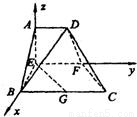 解:(Ⅰ)建立如图所示的空间坐标系,
解:(Ⅰ)建立如图所示的空间坐标系,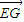 =(2,2,0),
=(2,2,0),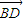 =(-2,2,2),(2分)
=(-2,2,2),(2分)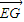 ,
,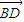 >=0,
>=0,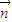 1=(x,y,z)则
1=(x,y,z)则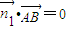 ,
,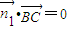 ,
,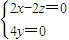 设x=1,即
设x=1,即 ,(7分)
,(7分)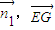 >=
>= ,
, ,
,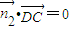 ,
,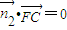 ,
,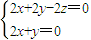 取x=1,
取x=1,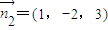 ,(12分)
,(12分)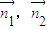 >=0,
>=0,

科目:高中数学 来源: 题型:
 如图,已知梯形ABCD中|AB|=2|CD|,点E分有向线段
如图,已知梯形ABCD中|AB|=2|CD|,点E分有向线段. |
| AC |
| 2 |
| 3 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:

 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:

 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积.
如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com