Question

已知函数f（x）=2^x，f^-1（x）是f（x）的反函数，那么f^-1（4-x²）的单调递减区间是（ ）
A．[0，+∞]
B．（-∞，0）
C．[0，2]
D．（-2，0）

Answer 1

【答案】分析：先依据求反函数的方法求出f（x）的解析式，再换元可得f ^-1（4-x²）的解析式，利用复合函数的单调性从而确定函数的单调减区间．
解答：解：∵f（x）=2^x的反函数为 f^-1（x）=log₂x，
∴f ^-1（x）=log₂x，
f ^-1（4-x²）=，
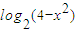
令t=4-x²，当t＞0时，得，-2＜x＜2，∴函数定义域为（-2，2）
根据二次函数单调性，对于函数t=4-x²，x的取值在对称轴右侧时为减函数，此时复合函数为减函数．
结合函数定义域，可得，当0＜x＜2时函数y=log₂（4-x²）为减函数
∴在（0，2）上函数值y=f^-1（4-x²）随自变量x的增大而减小，
故选C．
点评：本题考查求反函数的方法、函数单调性的应用、不等式的解法等基础知识，考查运算求解能力与转化思想．属于基础题．
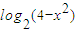