Question

15．若方程|x²-2x-1|-t=0有四个不同的实数根x₁，x₂，x₃，x₄，且x₁＜x₂＜x₃＜x₄，则2（x₄-x₁）+（x₃-x₂）的取值范围是（4$\sqrt{2}$，8+2$\sqrt{2}$）．

Answer 1

分析 方程|x²-2x-1|-t=0有四个不同的实数根x₁，x₂，x₃，x₄，实际上是抛物线y=|x²-2x-1|和直线y=t的四个不同的交点．根据根与系数的关系和不等式的性质进行解答．

解答 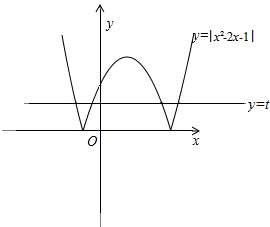解：如图，由|x²-2x-1|-t=0得到：t=|（x-1）²-2|，则0＜t＜2．
∴2＜2+t＜4.0＜2-t＜2．
∴4$\sqrt{2}$＜4$\sqrt{2+t}$＜8，0＜2$\sqrt{2-t}$＜2$\sqrt{2}$，
∴4$\sqrt{2}$＜4$\sqrt{2+t}$+2$\sqrt{2-t}$＜8+2$\sqrt{2}$．
∵方程|x²-2x-1|-t=0有四个不同的实数根x₁，x₂，x₃，x₄，x₁＜x₂＜x₃＜x₄，
∴x₁+x₄=x₂+x₃=2，x₁•x₄=-1-t，x₂•x₃=-1+t，
∴2（x₄-x₁）+（x₃-x₂）
=2$\sqrt{（{x}_{1}+{x}_{4}）^{2}-4{x}_{1}{x}_{4}}$+$\sqrt{（{x}_{2}+{x}_{3}）^{2}-4{x}_{2}{x}_{3}}$
=2$\sqrt{4+4（1+t）}$+$\sqrt{4-4（-1+t）}$
=4$\sqrt{2+t}$+2$\sqrt{2-t}$，
∴4$\sqrt{2}$＜2（x₄-x₁）+（x₃-x₂）＜8+2$\sqrt{2}$．
故答案是：（4$\sqrt{2}$，8+2$\sqrt{2}$）．

点评 本题主要考查一元二次方程根的情况和含有绝对值的函数的解法，考查基础知识的综合运用能力，以及数形结合的思想，属于中档题．