
9 2
分析:(A)把极坐标方程化为普通方程,利用点到直线的距离公式求出圆心(0,1)到直线的距离,此距离减去半径即为所求.
(B)先对
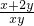
=
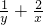
再将它乘以1结果保持不变,将2x+y=1看为一个整体代入得(
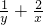
)×1=(
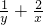
)×(2x+y),再展开后运用基本不等式可求得最小值.
(C)设内切圆半径为r,由勾股定理可得(1+r)
2+(2+r)
2=9,可得r
2+3r=2,再根据△ABC的面积为

×(1+r)(2+r),运算求得结果.
解答:(A)曲线ρ=2sinθ化为直角坐标方程为x
2+(y-1)
2=1,直线ρsin(θ+

)=4化为直角坐标方程为

x+y-8=0.
圆心(0,1)到直线的距离为 d=
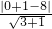
=

.则圆上的点到直线的最小距离为

-1=

.
即点A到直线ρsin(θ+

)=4的最小距离为

.
(B)解:∵2x+y=1,
∴
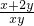
=
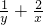
=(
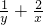
)×(2x+y)=5+
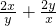
≥5+4=9
当且仅当
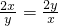
时等号成立,
则
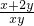
的最小值是 9.
(C)由于直角△ABC的内切圆与斜边AB相切于点D,且AD=1,BD=2,设内切圆半径为r,
则由勾股定理可得(1+r)
2+(2+r)
2=9,∴r
2+3r=2.
△ABC的面积为

×(1+r)(2+r)=

(r
2+3r+2)=2,
故答案为:

;9;2.
点评:A:本题考查把极坐标方程化为普通方程的方法,点到直线的距离公式的应用,直线和圆的位置关系.
B:本题考查基本不等式常见的变形形式与运用,如本题中,1的代换.在运用基本不等式时,要注意“一正、二定、三相等”的要求.
C:本题主要考查绝对值不等式的解法,直线和圆相交的性质,圆的切线性质、圆的参数方程,以及三角形中的几何计算,属于中档题.

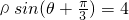 的距离的最小值是________.
的距离的最小值是________.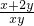 的最小值是________.
的最小值是________. 9 2
9 2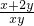 =
=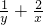 再将它乘以1结果保持不变,将2x+y=1看为一个整体代入得(
再将它乘以1结果保持不变,将2x+y=1看为一个整体代入得( 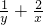 )×1=(
)×1=( 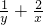 )×(2x+y),再展开后运用基本不等式可求得最小值.
)×(2x+y),再展开后运用基本不等式可求得最小值. ×(1+r)(2+r),运算求得结果.
×(1+r)(2+r),运算求得结果. )=4化为直角坐标方程为
)=4化为直角坐标方程为 x+y-8=0.
x+y-8=0.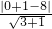 =
= .则圆上的点到直线的最小距离为
.则圆上的点到直线的最小距离为  -1=
-1= .
. )=4的最小距离为
)=4的最小距离为 .
.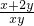 =
=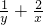 =(
=( 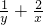 )×(2x+y)=5+
)×(2x+y)=5+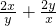 ≥5+4=9
≥5+4=9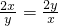 时等号成立,
时等号成立,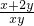 的最小值是 9.
的最小值是 9. ×(1+r)(2+r)=
×(1+r)(2+r)= (r2+3r+2)=2,
(r2+3r+2)=2, ;9;2.
;9;2.

 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)