Question

在等差数列{a_n}中，已知a₃+a₁₃=6，s₁₅=________．

Answer 1

45
分析：方法一：可以用a₁和d表示a₃+a₁₃=2（a₁+7d）以及S₁₅=15（a₁+7d），得出S₁₅=45
方法二：等差数列中，利用性质有a₁+a₁₅=a₃+a₁₃=45，再利用前n项和公式，得出S₁₅=45
解答：方法一：
∵数列{a_n}为等差数列
∴a₃+a₁₃=a₁+2d+a₁+12d=2a₁+14d=6
∴a₁+7d=3
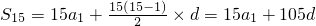
∵=15（a₁+7d）
∴S₁₅=15×3=45
故正确答案为 45
方法二：
∵数列{a_n}为等差数列
∴=
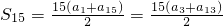
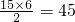
故正确答案为 45
点评：本题主要考查等差数列的通项公式、求和公式、等差数列的性质，体现了转化的数学思想．