
已知二次函数 (其中
(其中 )
)
(1)试讨论函数 的奇偶性.
的奇偶性.
(2)当 为偶函数时,若函数
为偶函数时,若函数 ,
,
试证明:函数 在
在 上单调递减,在
上单调递减,在 上单调递增;
上单调递增;
(1) 函数
函数 是非奇非偶函数
是非奇非偶函数
(2)见解析
【解析】本试题主要是考查了二次函数的性质,以及函数奇偶性和单调性的综合运用。
(1)函数 的定义域为R关于原点对称,………
的定义域为R关于原点对称,……… 
 故此时函数
故此时函数 是偶函数
是偶函数


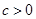 ,
, 故函数
故函数 不是奇函数,且易知此时
不是奇函数,且易知此时 故函数
故函数 也不是偶函数,所以
也不是偶函数,所以 函数
函数 是非奇非偶函数
是非奇非偶函数
(2)
 为偶函数,由(1)知
为偶函数,由(1)知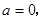
 利用定义法判定单调性。
利用定义法判定单调性。
解:(1) 函数 的定义域为R关于原点对称,………. 1分
的定义域为R关于原点对称,………. 1分

 故此时函数
故此时函数 是偶函数……….2分
是偶函数……….2分


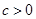 ,
, 故函数
故函数 不是奇函数,且易知此时
不是奇函数,且易知此时 故函数
故函数 也不是偶函数,所以
也不是偶函数,所以 函数
函数 是非奇非偶函数……….4分
是非奇非偶函数……….4分
(其他合理方式解答相应给分)
(2)
 为偶函数,由(1)知
为偶函数,由(1)知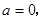
 ……….5分
……….5分
 ,则
,则 ……….7分
……….7分
=
 ……………9分
……………9分

 ,则
,则 <0
<0
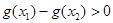 ,
, 
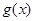 在
在 上单调递减, ……….11分
上单调递减, ……….11分
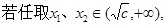
 ,则
,则 >0
>0
 <0 ,
<0 , 
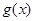 在
在 上单调递增, ……….13分
上单调递增, ……….13分


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源:2010-2011年广东省广州市高一下学期期末考试数学 题型:解答题
(本小题满分14分)
已知二次函数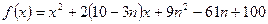 ,其中
,其中 .
.
(1)设函数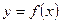 的图象的顶点的横坐标
的图象的顶点的横坐标 构成数列
构成数列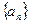 ,求证:数列
,求证:数列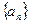 为等差数
为等差数 列;
列;
(2)设函数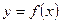 的图象的顶点到
的图象的顶点到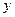 轴的距离构成数列
轴的距离构成数列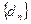 ,求数列
,求数列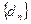 的前
的前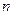 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2015届广东省高一上学期期中考试数学试卷(解析版) 题型:解答题
本小题满分10分
已知二次函数 (其中
(其中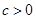 ).
).
(1)若函数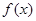 为偶函数,求
为偶函数,求 的值;
的值;
(2)当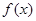 为偶函数时,若函数
为偶函数时,若函数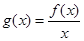 ,指出
,指出 在
在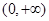 上单调性情况,并证明之.
上单调性情况,并证明之.
查看答案和解析>>
科目:高中数学 来源:2010-2011年广东省广州市高一下学期期末考试数学 题型:解答题
(本小题满分14分)
已知二次函数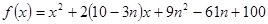 ,其中
,其中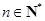 .
.
(1)设函数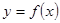 的图象的顶点的横坐标构成数列
的图象的顶点的横坐标构成数列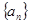 ,求证:数列
,求证:数列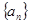 为等差数列;
为等差数列;
(2)设函数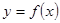 的图象的顶点到
的图象的顶点到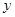 轴的距离构成数列
轴的距离构成数列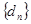 ,求数列
,求数列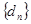 的前
的前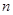 项和
项和 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com