设函数f(x)=ax2+bx+c(a,b,c∈R且a≠0)同时满足下列条件:①f(1)=1;②当x∈R时,恒有f(x)≥x成立;③当x∈R时,恒有f(x-4)=f(2-x)成立.
(1)求f(x)的表达式;
(2)设g(x)=4f(x)-4x+2,试问g(x)是否存在这样的区间[a,b](a<b)同时满足下列条件:①g(x)在[a,b]上单调;②若g(x)的定义域是[a,b],则其值域也是[a,b].若存在,求出这样的区间[a,b],若不存在,试说明理由.
【答案】
分析:(1)利用待定系数法结合题中条件,利用二次函数的性质建立关于a,b,c的方程求解即得;
(2)对于存在性问题,可先假设存在,即假设x存在这样的区间[a,b](a<b)同时满足两个条件,再利用函数的单调性,求出a,b的值,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(1)因当x∈R时,恒有f(x)≥x成立,
即ax
2+(b-1)x+c≥0,∴△=(b-1)
2-4ac≤0,且a>0,①
当x∈R时,恒有f(x-4)=f(2-x)成立,则函数f(x)=ax
2+bx+c和图象的对称轴是x=-1,
即-
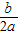
=-1,∴b=2a,②
又f(1)=1,∴a+b+c=1,③
由①②③解得:a=

,b=

,c=

,
∴f(x)的表达式为f(x)=

x
2+

x+

.
(2)g(x)=4f(x)-4x+2=x
2-2x+3,
假设存在这样的区间[a,b](a<b)同时满足下列条件:①g(x)在[a,b]上单调;②若g(x)的定义域是[a,b],则其值域也是[a,b].
∵g(x)在[a,b]上单调,∴a≥1或b≤1.
当a≥1时,g(x)在[a,b]上单调增,若g(x)的定义域是[a,b],则值域为[a
2-2a+3,b
2-2b+3],
∴
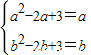
,此方程组无解;
当b≤1时,g(x)在[a,b]上单调减,若g(x)的定义域是[a,b],则值域为[b
2-2b+3,a
2-2a+3],
∴
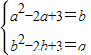
,此方程组无解;
综上可知,不存在这样的区间[a,b](a<b)同时满足条件.
点评:本小题主要考查函数单调性的应用、二次函数的性质、方程组的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

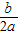 =-1,∴b=2a,②
=-1,∴b=2a,② ,b=
,b= ,c=
,c= ,
, x2+
x2+ x+
x+ .
.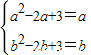 ,此方程组无解;
,此方程组无解;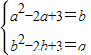 ,此方程组无解;
,此方程组无解;

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 设函数f(x)=(a
设函数f(x)=(a