
【题目】已知数列![]() 满足
满足![]() .
.
(1)证明:数列![]() 为等差数列;
为等差数列;
(2)设数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,且对任意的正整数n,都有
,且对任意的正整数n,都有![]() ,求整数
,求整数![]() 的值;
的值;
(3)设数列![]() 满足
满足![]() ,若
,若![]() ,且存在正整数s,t,使得
,且存在正整数s,t,使得![]() 是整数,求
是整数,求![]() 的最小值.
的最小值.
【答案】(1)证明见解析;(2)2;(3)![]()
【解析】
(1)令![]() 中的
中的![]() 为
为![]() ,又得一式,将两式做差变形,利用等差中项进行证明;
,又得一式,将两式做差变形,利用等差中项进行证明;
(2)利用放缩法和裂项相消法在数列求和中的应用进行证明.
(3)利用假设法的应用和存在性问题的应用求出最小值.
解:(1)因为![]() ①
①
所以![]() 时,
时,![]() ②
②
①-②得![]() ,
,
所以![]()
即![]()
所以数列![]() 为等差数列;
为等差数列;
(2)因为![]() ,所以
,所以![]() 的公差为1,
的公差为1,
因为对任意的正整数![]() ,都有
,都有![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 或2,
或2,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,这与题意矛盾,所以
,这与题意矛盾,所以![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,![]() 恒成立,
恒成立,
因为![]() ,
,
![]()
![]() ,
,
综上,![]() 的值为2.
的值为2.
(3)因为![]() ,所以
,所以![]() 的公差为
的公差为![]() ,
,
所以![]() ,
,
所以![]() ,
,
由题意,设存在正整数s,t,使得![]() ,
,![]() ,
,
则![]() ,即
,即![]() ,
,
因为![]() ,
,
所以![]() 是偶数,
是偶数,
所以![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,
,
所以存在![]() ,
,
综上,![]() 的最小值为
的最小值为![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】关于数列![]() ,给出下列命题:①数列
,给出下列命题:①数列![]() 满足
满足![]() ,则数列
,则数列![]() 为公比为2的等比数列;②“
为公比为2的等比数列;②“![]() ,
,![]() 的等比中项为
的等比中项为![]() ”是“
”是“![]() ”的充分不必要条件:③数列
”的充分不必要条件:③数列![]() 是公比为
是公比为![]() 的等比数列,则其前
的等比数列,则其前![]() 项和
项和![]() ;④等比数列
;④等比数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() ,
,![]() ,
,![]() 成等比数列,其中假命题的序号是( )
成等比数列,其中假命题的序号是( )
A.②B.②④C.①②④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试,若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.
(1)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;
(2)该校推荐选拔测试成绩在110以上的学生代表学校参加市知识竞赛,为了了解情况,在该校推荐参加市知识竞赛的学生中随机抽取2人,求选取的两人的选拔成绩在频率分布直方图中处于不同组的概率.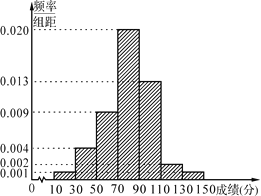
查看答案和解析>>
科目:高中数学 来源: 题型:
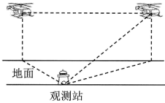
【题目】2019年10月1日,在庆祝新中国成立70周年阅兵中,由我国自主研制的军用飞机和军用无人机等参阅航空装备分秒不差飞越天安门,壮军威,振民心,令世人瞩目.飞行员高超的飞行技术离不开艰苦的训练和科学的数据分析.一次飞行训练中,地面观测站观测到一架参阅直升飞机以![]() 千米/小时的速度在同一高度向正东飞行,如图,第一次观测到该飞机在北偏西
千米/小时的速度在同一高度向正东飞行,如图,第一次观测到该飞机在北偏西![]() 的方向上,1分钟后第二次观测到该飞机在北偏东
的方向上,1分钟后第二次观测到该飞机在北偏东![]() 的方向上,仰角为
的方向上,仰角为![]() ,则直升机飞行的高度为________千米.(结果保留根号)
,则直升机飞行的高度为________千米.(结果保留根号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有人玩掷均匀硬币走跳棋的游戏,棋盘上标有第0站(出发地),在第1站,第2站,……,第100站. 一枚棋子开始在出发地,棋手每掷一次硬币,这枚棋子向前跳动一次,若掷出正向,棋子向前跳一站,若掷出反面,棋子向前跳两站,直到棋子跳到第99站(失败收容地)或跳到第100站(胜利大本营),该游戏结束. 设棋子跳到第![]() 站的概率为
站的概率为![]() .
.
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)写出![]() 与
与![]() 、
、![]() 的递推关系
的递推关系![]() );
);
(3)求玩该游戏获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)设点![]() 在
在![]() 轴上方,到线段
轴上方,到线段![]() 所在直线的距离为
所在直线的距离为![]() ,且
,且![]() ,求
,求![]() 和线段
和线段![]() 的大小;
的大小;
(2)设点![]() 为线段
为线段![]() 的中点,若
的中点,若![]() ,且点
,且点![]() 在第二象限内,求
在第二象限内,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
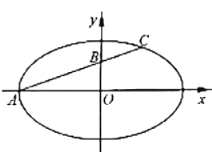
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,过
,过![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若椭圆![]() 的焦距为
的焦距为![]() ,
,![]() 为椭圆
为椭圆![]() 上一点,线段
上一点,线段![]() 的垂直平分线
的垂直平分线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() (
(![]() 不与
不与![]() 轴重合),求直线
轴重合),求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com