
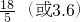
(0,1),或(2,1)
分析:(A)根据绝对值的意义求出不等式|x+1|-|x-2|>2的解集.
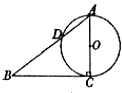
(B)设AD=xcm,由勾股定理可得 AB=10cm,再由圆的切割线定理可得64=10(10-x),由此求得x的值.
(C)把圆C的参数方程化为普通方程,把直线l的极坐标方程化为直角坐标方程,再代入圆的方程解的交点的坐标.
解答:(A)|x+1|-|x-2|表示数轴上的x对应点到-1对应点的距离减去它到2对应点的距离,而数轴上的

对应点到-1对应点的距离减去它到2对应点的距离正好等于2,
故不等式|x+1|-|x-2|>2的解集为
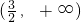
.
(B)设AD=x cm,∵Rt△ABC的两条直角边AC,BC的长分别为6cm,8cm,由勾股定理可得 AB=10 cm,
再由圆的切割线定理可得 BC
2=AB•BD,即 64=10(10-x),解得 x=3.6,
故答案为 3.6.
(C)圆C的参数方程
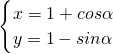
(α为参数),化为普通方程成为 (x-1)
2+(y-1)
2=1,
直线l的极坐标方程为ρsinθ=1,化为直角坐标方程为 y=1,代入圆的方程解得 x=0,或 x=2,
故点C 的坐标为 (0,1),或(2,1),
故答案为 (0,1),或(2,1).
点评:本题主要考查绝对值不等式的解法,圆的切割线定理的应用,把极坐标方程化为直角坐标方程的方法,求两曲线的交点坐标,属于中档题.

 (A)(不等式选做题)不等式|x+1|-|x-2|>2的解集为________.
(A)(不等式选做题)不等式|x+1|-|x-2|>2的解集为________.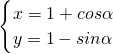 (α为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρsinθ=1,则直线l与圆C的交点的直角坐标是________.
(α为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρsinθ=1,则直线l与圆C的交点的直角坐标是________.
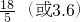 (0,1),或(2,1)
(0,1),或(2,1) 对应点到-1对应点的距离减去它到2对应点的距离正好等于2,
对应点到-1对应点的距离减去它到2对应点的距离正好等于2,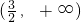 .
.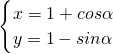 (α为参数),化为普通方程成为 (x-1)2+(y-1)2=1,
(α为参数),化为普通方程成为 (x-1)2+(y-1)2=1,

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案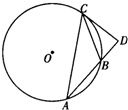 A.(不等式选做题)
A.(不等式选做题) A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为
A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) 选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)
选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)