选修4-5:不等式选讲
已知函数f(x)=|2x-m|+m.
(Ⅰ)若不等式f(x)≤6的解集为{x|-1≤x≤3},求实数m的值;
(Ⅱ)在(Ⅰ)的条件下,求使f(x)≤a-f(-x)有解的实数a的取值范围.
解:(Ⅰ)不等式f(x)≤6等价于|2x-m|+m≤6,即|2x-m|≤6-m.
∴m-6≤2x-m≤6-m
∴m-3≤x≤3
∵不等式f(x)≤6的解集为{x|-1≤x≤3},
∴m-3=-1,
∴m=2;
(Ⅱ)与(Ⅰ)知,f(x)=|2x-2|+2,令g(x)=f(x)+f(-x)
则g(x)=|2x-2|+|2x+2|+4=
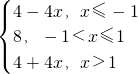
∵x≤-1时,4-4x≥8;x>1时,4+4x>8
∴g(x)的最小值为8
∴使f(x)≤a-f(-x)有解的实数a的取值范围[8,+∞).
分析:(Ⅰ)不等式f(x)≤6等价于|2x-m|+m≤6,即|2x-m|≤6-m,利用不等式f(x)≤6的解集为{x|-1≤x≤3},即可求实数m的值;
(Ⅱ)令g(x)=f(x)+f(-x),确定其最小值,即可求得使f(x)≤a-f(-x)有解的实数a的取值范围.
点评:本题考查绝对值函数,考查解绝对值不等式,解题的关键是确定函数的最小值,属于中档题.

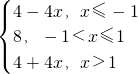


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案