
【题目】下列命题中的假命题是( )
A.?x∈R,2﹣x+1>1
B.?x∈[1,2],x2﹣1≥0
C.?x∈R,sinx+cosx= ![]()
D.?x∈R,x2+ ![]() ≤1
≤1
科目:高中数学 来源: 题型:
【题目】已知圆C的方程为(x﹣3)2+y2=1,圆M的方程为(x﹣3﹣3cosθ)2+(y﹣3sinθ)2=1(θ∈R),过M上任意一点P作圆C的两条切线PA,PB,切点分别为A、B,则∠APB的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某加工厂用某原料由车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天功能完成至多70多箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为( )
A.甲车间加工原料10箱,乙车间加工原料60箱
B.甲车间加工原料15箱,乙车间加工原料55箱
C.甲车间加工原料18箱,乙车间加工原料50箱
D.甲车间加工原料40箱,乙车间加工原料30箱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x﹣ ![]() sin2x+asinx在(﹣∞,+∞)单调递增,则a的取值范围是( )
sin2x+asinx在(﹣∞,+∞)单调递增,则a的取值范围是( )
A.[﹣1,1]
B.[﹣1, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣1,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣ax﹣1(a∈R).
(1)若对任意实数x,f(x)<0恒成立,求实数a的取值范围;
(2)当a>0时,解关于x的不等式f(x)<2x﹣3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差不为0的等差数列,数列{bn}是等比数列,且b1=a1=1,b2=a3 , b3=a9
(1)求数列{an}的通项公式;
(2)求数列{anbn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R.当x<0时,f(x)=x3﹣1;当﹣1≤x≤1时,f(﹣x)=﹣f(x);当x> ![]() 时,f(x+
时,f(x+ ![]() )=f(x﹣
)=f(x﹣ ![]() ).则f(6)=( )
).则f(6)=( )
A.﹣2
B.﹣1
C.0
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在单调递增数列{an}中,a1=2,a2=4,且a2n﹣1 , a2n , a2n+1成等差数列,a2n , a2n+1 , a2n+2成等比数列,n=1,2,3,….
(Ⅰ)(ⅰ)求证:数列 ![]() 为等差数列;
为等差数列;
(ⅱ)求数列{an}的通项公式.
(Ⅱ)设数列 ![]() 的前n项和为Sn , 证明:Sn>
的前n项和为Sn , 证明:Sn> ![]() ,n∈N* .
,n∈N* .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( ) 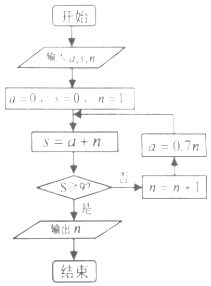
A.4
B.5
C.6
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com