
【题目】我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( ) 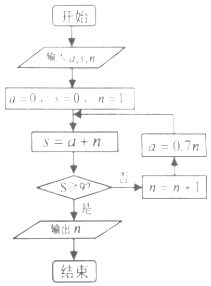
A.4
B.5
C.6
D.7
【答案】C
【解析】解:模拟执行程序,可得 a=0,S=0,n=1
S=1
不满足条件S≥9,执行循环体,n=2,a=1.4,S=3.4
不满足条件S≥9,执行循环体,n=3,a=2.1,S=5.1
不满足条件S≥9,执行循环体,n=4,a=2.8,S=6.8
不满足条件S≥9,执行循环体,n=5,a=3.5,S=8.5,
不满足条件S≥9,执行循环体,n=6,a=4.2,S=10.2,
退出循环,输出n的值为6.
故选:C
【考点精析】关于本题考查的程序框图,需要了解程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明才能得出正确答案.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】下列命题中的假命题是( )
A.?x∈R,2﹣x+1>1
B.?x∈[1,2],x2﹣1≥0
C.?x∈R,sinx+cosx= ![]()
D.?x∈R,x2+ ![]() ≤1
≤1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】锐角△ABC中,其内角A、B满足:2cosA=sinB﹣ ![]() cosB.
cosB.
(1)求角C的大小;
(2)D为AB的中点,CD=1,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=4,an+1=qan+d(q,d为常数).
(1)当q=1,d=2时,求a2017的值;
(2)当q=3,d=﹣2时,记 ![]() ,Sn=b1+b2+b3+…+bn , 证明:
,Sn=b1+b2+b3+…+bn , 证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《张丘建算经》是我国南北朝时期的一部重要数学著作,书中系统的介绍了等差数列,同类结果在三百多年后的印度才首次出现.书中有这样一个问题,大意为:某女子善于织布,后一天比前一天织的快,而且每天增加的数量相同,已知第一天织布5尺,一个月(按30天计算)总共织布390尺,问每天增加的数量为多少尺?该问题的答案为( )
A.![]() 尺
尺
B.![]() 尺
尺
C.![]() 尺
尺
D.![]() 尺
尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l: 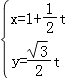 (t为参数),曲线C1:
(t为参数),曲线C1: ![]() (θ为参数).
(θ为参数).
(Ⅰ)设l与C1相交于A,B两点,求|AB|;
(Ⅱ)若把曲线C1上各点的横坐标压缩为原来的 ![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的 ![]() 倍,得到曲线C2 , 设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
倍,得到曲线C2 , 设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击.已知缉私艇的最大航速是走私船最大航速的3倍.假设缉私艇和走私船均按直线方向以最大航速航行.(参考数据: ![]() °
° ![]() ,
, ![]() )
)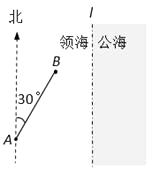
(1)若走私船沿正东方向逃离,试确定缉私艇的追击方向,使得用最短时间在领海内拦截成功;
(2)问:无论走私船沿何方向逃跑,缉私艇是否总能在领海内成功拦截?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com