
【题目】锐角△ABC中,其内角A、B满足:2cosA=sinB﹣ ![]() cosB.
cosB.
(1)求角C的大小;
(2)D为AB的中点,CD=1,求△ABC面积的最大值.
【答案】
(1)解:∵2cosA+ ![]() cosB=sinB,可得:cosA=
cosB=sinB,可得:cosA= ![]() sinB﹣
sinB﹣ ![]() cosB=cos(
cosB=cos( ![]() ﹣B),
﹣B),
又∵A,B为锐角,
∴0 ![]() ,
, ![]() <
< ![]() ﹣B<
﹣B< ![]() ,
,
∴A= ![]() ﹣B,A+B=
﹣B,A+B= ![]() ,可得:C=π﹣
,可得:C=π﹣ ![]() =
= ![]()
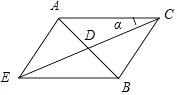
(2)解:设∠ACD=α,延长CD到E,使CD=DE,
则AEBC为平行四边形,
在△ACE中,AC=b,AE=BC=α,CE=2,∠CAE= ![]() ,∠AEC=
,∠AEC= ![]() ﹣α,
﹣α,
由正弦定理可得: 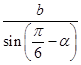 =
= ![]() =
= ![]() ,
,
所以,a=4sinα,b=4sin( ![]() ﹣α),
﹣α),
S△ABC= ![]() absin∠ABC=
absin∠ABC= ![]() sin
sin ![]()
=4sinαsin( ![]() ﹣α)=2sinαcosα﹣2
﹣α)=2sinαcosα﹣2 ![]() sin2α
sin2α
=sin2α+ ![]() cos2α﹣
cos2α﹣ ![]() =2sin(2α+
=2sin(2α+ ![]() )﹣
)﹣ ![]() ,
,
当α= ![]() 时,△ABC的面积取得最大值,最大值为2﹣
时,△ABC的面积取得最大值,最大值为2﹣ ![]() .
.
【解析】(1)由已知利用特殊角的三角函数值,两角差的正弦函数公式可得cosA=cos( ![]() ﹣B),结合A,B为锐角,利用三角形内角和定理可求C的值.(2)设∠ACD=α,延长CD到E,使CD=DE,则AEBC为平行四边形,在△ACE中,由正弦定理可得a=4sinα,b=4sin(
﹣B),结合A,B为锐角,利用三角形内角和定理可求C的值.(2)设∠ACD=α,延长CD到E,使CD=DE,则AEBC为平行四边形,在△ACE中,由正弦定理可得a=4sinα,b=4sin( ![]() ﹣α),利用三角形面积公式,三角函数恒等变换的应用化简可得S△ABC=2sin(2α+
﹣α),利用三角形面积公式,三角函数恒等变换的应用化简可得S△ABC=2sin(2α+ ![]() )﹣
)﹣ ![]() ,利用正弦函数的性质可求△ABC面积的最大值.
,利用正弦函数的性质可求△ABC面积的最大值.
【考点精析】本题主要考查了正弦定理的定义的相关知识点,需要掌握正弦定理:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣ax﹣1(a∈R).
(1)若对任意实数x,f(x)<0恒成立,求实数a的取值范围;
(2)当a>0时,解关于x的不等式f(x)<2x﹣3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}满足a1=1,an+an+1=( ![]() )n(n∈N*),Sn=a1+4a2+42a3+…+4n﹣1an , 则5Sn﹣4nan=( )
)n(n∈N*),Sn=a1+4a2+42a3+…+4n﹣1an , 则5Sn﹣4nan=( )
A.n﹣1
B.n
C.2n
D.n2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD= ![]() CD=2,点M是EC中点. (Ⅰ)求证:BM∥平面ADEF;
CD=2,点M是EC中点. (Ⅰ)求证:BM∥平面ADEF;
(Ⅱ)求三棱锥M﹣BDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( ) 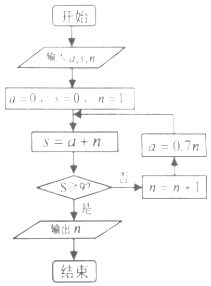
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,在直角梯形ABCD中, ![]() ,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示. 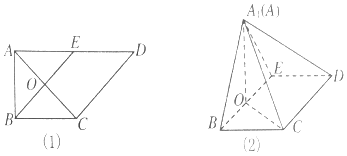
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com